top of page
Ara


Aktör-Gözlemci Yanlılığı Nedir?
Aktör-gözlemci yanlılığı, bireyin kendi davranışlarını dışsal nedenlere , başkalarının davranışlarını ise içsel özelliklere bağlama eğilimidir. Yani kişi, kendi yaptığı bir hatayı çoğunlukla koşullarla açıklarken, başkasının yaptığı aynı hatayı karakter özellikleriyle açıklar. Bu durum, sosyal ilişkilerde yanlış anlamalara, önyargılara ve adaletsiz değerlendirmelere yol açabilir. Günlük Hayattan Basit Bir Örnek Yolda yürürken kayıp düşersen: “Zemin çok kaygandı” dersin. Bu,
Nominal Analiz
22 Oca4 dakikada okunur


İstatistiksel Analiz Nedir ve Araştırma Sürecinde Nasıl Uygulanır?
İstatistiksel analiz, nicel veriler kullanarak eğilimleri, örüntüleri ve değişkenler arasındaki ilişkileri inceleme sürecidir . Bilim insanları, kamu kurumları, işletmeler ve birçok farklı kuruluş için temel bir araştırma aracıdır. Geçerli ve güvenilir sonuçlara ulaşabilmek için istatistiksel analiz, araştırma sürecinin en başından itibaren planlanmalıdır . Bunun için: Araştırma hipotezlerini tanımlamak, Araştırma desenine karar vermek, Örneklem büyüklüğünü ve örnekleme yönte
Nominal Analiz
7 Ara 20258 dakikada okunur


Merkezi Limit Teoremi: Tanım, Formül ve Örnekler
🔍 Merkezi Limit Teoreminin Temel Tanımı Merkezi limit teoremi, bir evrenden yeterince büyük örneklemler alındığında bu örneklemlerin örneklem ortalamalarının dağılımının her zaman normal dağılıma yakınsadığını ifade eder. Bu durum, evrenin Poisson, binom, sürekli çarpık ya da başka bir dağılıma sahip olmasından bağımsızdır. Örnek Poisson dağılımına sahip bir evrenden 50 birimlik 10.000 örneklem alındığında, örneklem ortalamalarının dağılımı normal bir yapı gösterir. 📊 Me
Nominal Analiz
7 Ara 20253 dakikada okunur


Etki Büyüklüğü Nedir ve Araştırmalarda Neden Önemlidir?
🔍 Etki Büyüklüğünün Araştırmadaki Rolü Etki büyüklüğü, değişkenler arasındaki ilişkinin veya gruplar arasındaki farkın gerçek dünyadaki anlamlılığını ifade eder. Bir bulgunun sadece istatistiksel olarak anlamlı olup olmadığını değil, ne kadar önemli ve uygulanabilir olduğunu göstermesi açısından kritik öneme sahiptir. Büyük etki büyüklüğü: Bulguların pratikte anlamlı olduğunu gösterir. Küçük etki büyüklüğü: Uygulamada sınırlı bir katkı olduğunu gösterir. İstatistiksel an
Nominal Analiz
6 Ara 20253 dakikada okunur


Serbestlik Derecesi: Tanımı, Hesaplanması ve İstatistiksel Testlerdeki Rolü
📌 Serbestlik Derecesinin Temel Tanımı Serbestlik derecesi, istatistiksel bir değeri hesaplarken kullanılan bağımsız bilgi parçacıklarının sayısını ifade eder. Genellikle v veya df ile gösterilir ve temel formülü şöyledir: df = örneklem büyüklüğü − kısıtlama sayısı Bu kavram, istatistiksel bir testin sonuçlarının değerlendirilmesinde kritik öneme sahiptir. Serbestlik dereceleri, test istatistiğinin yanında parantez içinde raporlanır ve kullanılan dağılımın şeklini belirler
Nominal Analiz
6 Ara 20254 dakikada okunur


Tip I ve Tip II Hatalar: Tanımlar, Farklar ve İstatistiksel Bağlam
🔍 İstatistiksel Karar Verme Sürecinde Hata Kavramı Hipotez testlerinde verilen kararlar her zaman belirli bir belirsizlik içerir. Bu nedenle yanlış sonuca ulaşma riski kaçınılmazdır. Bu yanlış sonuçlar Tip I hata veya Tip II hata şeklinde ortaya çıkar. Tip I hata: Yanlış bir biçimde olumlu sonuç elde edilmesi (yanlış pozitif). Tip II hata: Yanlış bir biçimde olumsuz sonuç elde edilmesi (yanlış negatif). Tip I hata olasılığı alfa (α) , Tip II hata olasılığı ise beta (β)
Nominal Analiz
6 Ara 20254 dakikada okunur


Yokluk ve Karşıt Hipotezlerin Farkları ve Yazım Biçimleri
Hipotezlerin Araştırma Sorusuyla İlişkisi Yokluk hipotezi ve karşıt hipotez, bir araştırma sorusuna verilen iki farklı cevabı temsil eder. Her ikisi de evren hakkında iddialar ortaya koyar ve her biri istatistiksel testler aracılığıyla değerlendirilir. Araştırma sorusunda “Bağımsız değişken bağımlı değişkeni etkiler mi?” sorusu yer alıyorsa: Yokluk hipotezi: Etkinin olmadığı iddiasını taşır. Karşıt hipotez: Etkinin bulunduğu iddiasını sunar. Her iki hipotez de örneklemden e
Nominal Analiz
30 Kas 20252 dakikada okunur


Yokluk (H0) (Null) ve Karşıt (Alternatif) Hipotez: Nedir, Ne İşe Yarar ve Nasıl Yazılır?
Araştırma Sorusunun Hipotezlerle Yanıtlanması Yokluk hipotezi ve karşıt hipotez, araştırma sorusuna verilen iki rakip yanıtı temsil eder. Araştırma sorusu “Bağımsız değişken bağımlı değişkeni etkiler mi?” şeklindeyse: Yokluk hipotezi bu soruya “Hayır, etkisi yoktur” yanıtını verir. Karşıt hipotez ise “Evet, bir etki vardır” şeklinde karşı iddiayı sunar. Bu iki hipotez her zaman evren hakkında kurulur. Çünkü hipotez testinin amacı, örneklemden hareketle evren hakkında çıkar
Nominal Analiz
30 Kas 20254 dakikada okunur

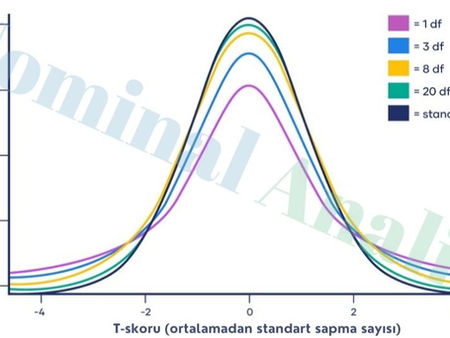
T Dağılımı: Nedir, Ne İşe Yarar ve İstatistiksel Analizlerde Nasıl Kullanılır?
T Dağılımının Genel Yapısı T dağılımı, grafiğe aktarıldığında çan şeklini izleyen ve gözlemlerin çoğunun ortalamaya yakın, uçlarda ise daha seyrek olduğu bir veri dağılımını tanımlar. Bu dağılım, özellikle örneklem büyüklüğünün küçük olduğu durumlarda ve varyansın bilinmediği veri yapılarında kullanılır. Normal dağılıma benzeyen bir form gösterse de daha temkinli bir olasılık dağılımı sunar. Merkezdeki olasılığı azaltırken uçlara verilen olasılığı artırarak küçük örneklemlerd
Nominal Analiz
29 Kas 20253 dakikada okunur


Poisson Dağılımı: Tanım, Formül ve Örneklerle Kapsamlı Açıklama
Poisson dağılımı, belirli bir zaman ya da alan aralığında bir olayın kaç kez gerçekleştiğini modelleyen ayrık bir olasılık dağılımıdır. Olaylar rastgele ve birbirinden bağımsız gerçekleşiyorsa, ve belirli bir aralık için ortalama olay sayısı biliniyorsa, Poisson dağılımı bu olayların olasılık yapısını başarılı şekilde açıklar. Dağılımın tek parametresi vardır: λ (lambda) . Bu değer hem beklenen olay sayısını (ortalama) hem de varyansı temsil eder. Bu özellik Poisson dağılım
Nominal Analiz
29 Kas 20253 dakikada okunur

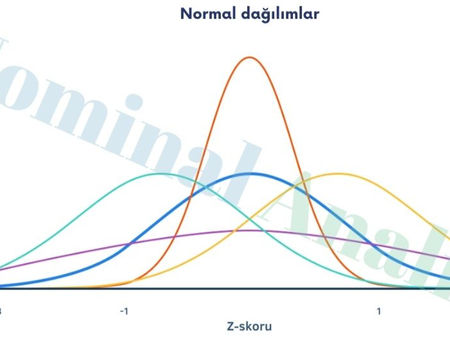
Standart Normal Dağılımı (Z-Dağılımı): Tanım, Kullanım Alanları ve Örneklerle Açıklama
Standart normal dağılım, istatistikte en sık kullanılan olasılık dağılımlarından biridir. Ortalama değerin ( 0 ) ve standart sapmanın ( 1 ) olduğu özel bir normal dağılım türüdür. Bu özel yapı sayesinde veri noktalarının standart hatalar cinsinden ifade edilmesine, olasılıkların hesaplanmasına ve farklı veri setlerinin karşılaştırılmasına olanak sağlar. Her normal dağılım, uygun dönüşümle standart normal dağılıma dönüştürülebilir. Bu dönüşüm “z-skoru” olarak bilinir ve tüm he
Nominal Analiz
29 Kas 20252 dakikada okunur


Normal Dağılım: Özellikleri, Kullanım Alanları ve Hesaplama Mantığı
Normal dağılım, istatistik ve bilimsel araştırmalarda en sık karşılaşılan dağılımlardan biridir. Verilerin büyük kısmının bir merkezin etrafında toplandığı, uçlara doğru gidildikçe gözlem sayısının azaldığı karakteristik bir yapıya sahiptir. Grafiğe döküldüğünde simetrik bir çan eğrisi oluştuğu için çan eğrisi veya Gaussian dağılımı olarak da bilinir. Bu yazıda normal dağılımın temel özelliklerini, neden önemli olduğunu, hangi durumlarda kullanıldığını ve nasıl hesaplandığı
Nominal Analiz
28 Kas 20253 dakikada okunur


T-Dağılımı (Student’s t-Distribution): Küçük Örneklemler İçin Güçlü Bir İstatistiksel Araç
T-dağılımı, özellikle küçük örneklemlerle çalışırken ve popülasyon varyansı bilinmediğinde kullanılan özel bir olasılık dağılımıdır. Şekil olarak normal dağılıma benzese de, kuyrukları daha geniştir ve uç değerlere daha fazla olasılık tanır. Bu özellik, küçük örneklemlerde belirsizliğin daha yüksek olmasını doğru bir şekilde yansıtır. İstatistiksel analizlerde t-dağılımı en çok güven aralıklarını hesaplamak ve t-testlerinde p-değerlerini bulmak için kullanılır. T-Dağılımı
Nominal Analiz
28 Kas 20253 dakikada okunur


Ölçme Düzeyleri: Nominal, Ordinal, Aralık ve Oran Düzeyleri
İstatistikte ölçme düzeyleri, değişkenlerin hangi hassasiyetle ölçüldüğünü ve bu değişkenlere hangi analizlerin uygulanabileceğini belirler. Bir değişkenin ölçme düzeyi, araştırmanın planlanmasından veri analiz sürecine kadar tüm aşamaları doğrudan etkiler. Dolayısıyla ölçme düzeylerinin mantığını anlamak, doğru yöntemlerle doğru sonuçlara ulaşmanın temelidir. Bu yazıda ölçme düzeylerinin ne olduğunu, nasıl sınıflandırıldığını ve analiz sürecini nasıl şekillendirdiğini detayl
Nominal Analiz
24 Kas 20254 dakikada okunur


Standart Sapma Nasıl Hesaplanır? | Tanım, Mantık ve Örneklerle Açıklama
Standart sapma, bir veri setindeki değerlerin ortalamadan ne kadar uzaklaştığını gösteren en önemli değişkenlik ölçülerinden biridir. Başka bir ifadeyle, değerlerin ortalamadan ortalama uzaklığıdır . Eğer bir veri setinde değerler birbirine yakınsa standart sapma düşüktür; değerler daha dağınık ve birbirinden uzaksa standart sapma yüksektir. Bu ölçü özellikle normal dağılımlar için çok bilgilendiricidir ve psikoloji, eğitim bilimleri, sağlık araştırmaları, mühendislik ve eko
Nominal Analiz
24 Kas 20253 dakikada okunur


Interquartile Range (IQR) (Çeyrekler Arası Aralık): Orta %50’lik Dağılımın Gücünü Anlama Rehberi
İstatistikte bir veri setini anlamanın iki temel yolu vardır: (1) Verilerin merkezi eğilimi, (2) Verilerin yayılımı. Yayılım ölçüleri arasında ise IQR – Interquartile Range (Çeyrekler Arası Aralık) , özellikle uç değerlerin yoğun olduğu veya çarpık dağılımlarda en güvenilir göstergelerden biri olarak öne çıkar. IQR, veri setinin orta yarısının (yani %25 ile %75 arasında kalan kısmının) ne kadar yayıldığını gösterir. Bu nedenle hem veri temizleme süreçlerinde hem de dağıl
Nominal Analiz
24 Kas 20253 dakikada okunur


Veri Setinde Range (Değer Aralığı) Nasıl Bulunur? | Tanım, Örnekler ve Açıklama
Veri analizi yaparken yalnızca ortalamayı bilmek yeterli değildir; aynı zamanda verilerin ne kadar yayıldığını, yani birbirinden ne kadar uzaklaştığını da anlamak gerekir. İşte tam bu noktada range (değer aralığı) devreye girer. Range, bir veri setindeki en büyük değer ile en küçük değer arasındaki farkı gösteren, yorumlaması son derece kolay bir değişkenlik ölçüsüdür. Bu yazıda range kavramını, nasıl hesaplandığını, ne zaman kullanılabileceğini ve ne zaman yanıltıcı olabil
Nominal Analiz
24 Kas 20253 dakikada okunur


Dağılım Ölçüleri: Aralık, Çeyrekler Arası Aralık, Varyans ve Standart Sapma Nedir?
Veri analizi yapılırken, sadece merkezi eğilim ölçülerini (ortalama, medyan, mod) bilmek tek başına yeterli değildir. Bir veri setinin gerçek yapısını anlayabilmek için, değerlerin birbirinden ne kadar uzaklaştığını , yani dağılımın genişliğini bilmek gerekir. Bu genişliği ölçen kavram değişkenlik (variability) olarak adlandırılır. Değişkenlik; veri noktalarının birbirinden ve dağılımın merkezinden ne kadar farklı olduğunu gösterir. Bu nedenle hem tanımlayıcı istatistiklerd
Nominal Analiz
24 Kas 20253 dakikada okunur


Geometrik Ortalama Nedir? Nasıl Hesaplanır ve Ne Zaman Kullanılır?
Geometrik ortalama, bir veri setindeki değerlerin çarpımının n’inci kökünün alınmasıyla elde edilen özel bir merkezi eğilim ölçüsüdür. En sık kullanılan aritmetik ortalamadan farklı olarak, geometrik ortalama değerleri toplamak yerine çarpma işlemi üzerine kuruludur . Bu özellik, özellikle büyüme oranları, yüzdesel değişimler ve geniş aralıklı verilerin analizinde büyük avantaj sağlar. Geometrik Ortalama Neden Önemlidir? Aritmetik ortalama bağımsız değerler için uygunken, ge
Nominal Analiz
24 Kas 20252 dakikada okunur


İstatistikte Mod Nedir? | Tanım, Örnekler ve Kullanım Alanları
Mod (modal değer), bir veri setinde en sık tekrar eden değeri ifade eden merkezi eğilim ölçüsüdür. Bir başka deyişle, bir grubun içinde en çok görülen özellik, tercih veya sayı mod olarak adlandırılır. İstatistikte mod; özellikle kategorik verileri anlamlandırmada, en yaygın seçeneği belirlemede ve dağılımın genel yapısını tanımlamada sıkça kullanılır. Mod, üç temel merkezi eğilim ölçüsünden biridir: Mod : En sık görülen değer Medyan : Ortadaki değer Aritmetik Ortalama (Mean
Nominal Analiz
24 Kas 20253 dakikada okunur
bottom of page




