Standart Normal Dağılımı (Z-Dağılımı): Tanım, Kullanım Alanları ve Örneklerle Açıklama

Standart normal dağılım, istatistikte en sık kullanılan olasılık dağılımlarından biridir. Ortalama değerin (0) ve standart sapmanın (1) olduğu özel bir normal dağılım türüdür. Bu özel yapı sayesinde veri noktalarının standart hatalar cinsinden ifade edilmesine, olasılıkların hesaplanmasına ve farklı veri setlerinin karşılaştırılmasına olanak sağlar.

Her normal dağılım, uygun dönüşümle standart normal dağılıma dönüştürülebilir. Bu dönüşüm “z-skoru” olarak bilinir ve tüm hesaplamaların ortak bir ölçekte yapılmasını mümkün kılar.

Normal Dağılım ve Standart Normal Dağılım Arasındaki Fark

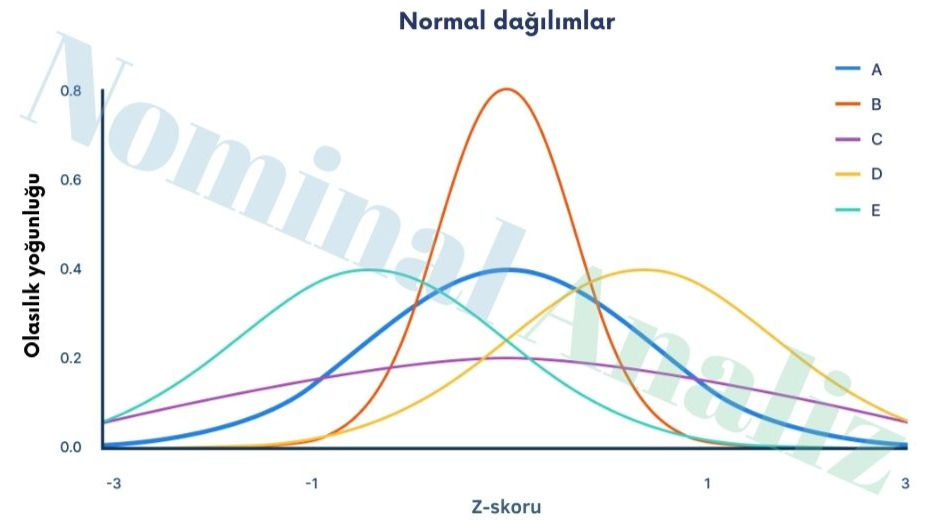
Her iki dağılım da çan eğrisi şeklinde, simetrik ve tek tepe noktalıdır. Ancak aralarında iki önemli fark vardır:

1. Ortalama (μ)

• Normal dağılımlarda herhangi bir değer olabilir.

• Standart normal dağılımda her zaman 0’dır.

2. Standart Sapma (σ)

• Normal dağılımlar için istediğiniz pozitif değerde olabilir.

• Standart normal dağılımda her zaman 1’dir.

Bu fark nedeniyle, standart normal dağılım tüm normal dağılımların referans formudur.

Akademik Danışmanlık

SPSS Analizi & Görselleştirilmiş Rapor

Hizmeti Satın Al

Z-Skoru Nedir?

Bir z-skoru, bir veri noktasının ortalamadan kaç standart sapma uzakta olduğunu gösterir.

Z-skoru formülü:

Z-Skoru Nasıl Hesaplanır? (Örnek)

Bir öğrenci grubunun SAT puanlarının:

• Ortalama = 1150

• Standart sapma = 150

olduğunu varsayalım.

Bir öğrencinin puanı: 1380

Bu, 1380 puanın ortalamanın 1.53 standart sapma üzerinde olduğunu gösterir.

Standart Normal Dağılımda Olasılık Hesaplama

Standart normal dağılımın altında kalan alan, bir olasılığı temsil eder. Bunun için z-tablosu veya bir çevrimiçi hesaplayıcı kullanılır.

Önceki örnekteki z = 1.53 değeri için:

• Z-tablosundaki değer: 0.937

Bu, 1380 veya daha düşük puan alma olasılığının %93.7 olduğunu gösterir.

Üst taraf olasılığı (x > 1380)

1 − 0.937 = 0.063

Yani öğrencilerin yalnızca %6.3’ü 1380 üzeri puan alır.

Standart Normal Dağılımın Kullanım Alanları

1. Olasılık Hesaplama

Belirli bir değerin üzerinde veya altında gözlem oluşma olasılığı bulunur.

2. Z-Testleri

Z-skoru, hipotez testlerinde kullanılan test istatistiğidir.

• Grup ortalamasının referans bir popülasyon ortalamasından farklı olup olmadığını inceler.

• Normal dağılım ve bilinen popülasyon standart sapması varsayımı gerekir.

3. Farklı Ölçeklerdeki Veri Setlerini Karşılaştırma

Örneğin:

• Boy (cm)

• Sınav puanı

• Gelir (₺)

gibi farklı değişkenler z-skoru üzerinden ortak bir ölçekte karşılaştırılabilir.

4. Puan Normalizasyonu (Eğriye Göre Not Verme)

Eğitim ve ölçme-değerlendirme alanında yaygın kullanım alanına sahiptir.

Z-Tablosu Nasıl Kullanılır?

Z-tablosu, her z-skoru için eğrinin sol tarafında kalan toplam alanı verir.

Örneğin:

• Z = 2.24 için tablo değeri: 0.9874

Bu demektir ki:

• Gözlem, popülasyonun %98.74’ünden daha yüksektir.

• Üstte kalan alan (p-değeri):

  1−0.9874=0.01261 - 0.9874 = 0.01261−0.9874=0.0126

• p < 0.05 olduğundan sonuç istatistiksel olarak anlamlıdır.

Araştırma Örneği: Z-Testi Uygulaması

Bir uyku araştırmasında:

• Pandemi öncesi ortalama uyku süresi = 6.5 saat

• Standart sapma = 0.5

• Pandemi döneminde ölçülen örneklem ortalaması = 7.62

• Örneklem büyüklüğü = büyük

1. Z-skorunun hesaplanması

2. Z-tablosundan p-değeri bulunması

p = 1− 0.9874 = 0.0126

Bu değer 0.05’ten küçük olduğundan, pandemi döneminde uyku süresinin anlamlı şekilde arttığı söylenebilir.

Standart Normal Dağılımın Önemi

• Parametrik testlerin temelinde yer alır.

• Popülasyon davranışını tahmin etmek için güçlü bir model sağlar.

• Örneklem ortalamalarının dağılımını açıklayan merkezi limit teoremi ile bağlantılıdır.

• Z-skorları sayesinde istatistiksel kararlar objektif şekilde verilebilir.