Merkezi Limit Teoremi: Tanım, Formül ve Örnekler

🔍 Merkezi Limit Teoreminin Temel Tanımı

Merkezi limit teoremi, bir evrenden yeterince büyük örneklemler alındığında bu örneklemlerin örneklem ortalamalarının dağılımının her zaman normal dağılıma yakınsadığını ifade eder.

Bu durum, evrenin Poisson, binom, sürekli çarpık ya da başka bir dağılıma sahip olmasından bağımsızdır.

Örnek

Poisson dağılımına sahip bir evrenden 50 birimlik 10.000 örneklem alındığında, örneklem ortalamalarının dağılımı normal bir yapı gösterir.

📊 Merkezi Limit Teoremi Neyi Açıklar?

Teoremin temelinde örnekleme dağılımı kavramı yer alır. Bu kavramı anlamak için aşağıdaki düşünce deneyini izlemek yardımcı olabilir:

1. Evrenden rastgele bir örneklem çek ve örneklem ortalamasını hesapla.

2. Aynı büyüklükte ikinci bir örneklem çek ve tekrar ortalamayı hesapla.

3. Bu işlemi çok sayıda örneklem için tekrarla.

Ortalamaların dağılımı, örnekleme dağılımıdır ve merkezi limit teoremine göre örneklem büyüklüğü yeterince büyükse normal dağılıma dönüşür.

📐 Merkezi Limit Teoreminin Formülü

Örnekleme dağılımının parametreleri, evrenin parametrelerine bağlıdır:

Örnekleme dağılımının ortalaması

Örnekleme dağılımının standart sapması

Örneklem ortalamasının dağılımı

Burada:

📏 Örneklem Büyüklüğü ve Merkezi Limit Teoremi

Örneklem büyüklüğü, örnekleme dağılımını iki şekilde etkiler.

1. Örneklem büyüklüğü ve normal dağılıma yakınsama

• n < 30: Örnekleme dağılımı normal olmak zorunda değildir, evrenin dağılımına benzer.

• n ≥ 30: Merkezi limit teoremi uygulanabilir; örnekleme dağılımı yaklaşık normal olur.

2. Örneklem büyüklüğü ve standart sapma

Standart sapma, dağılımın ne kadar “yayvan” olduğunu gösterir.

• n küçükse: Yayılım geniştir, örneklem ortalamaları değişkendir.

• n büyükse: Yayılım daralır, örneklem ortalamaları daha isabetli tahminler sunar.

🧩 Merkezi Limit Teoreminin Geçerli Olma Koşulları

Teorem şu üç koşul altında geçerlidir:

• Örneklem büyüklüğü yeterince büyük olmalıdır (genelde n ≥ 30).

• Örneklemler bağımsız ve aynı dağılımdan gelmelidir (i.i.d).

• Evrende varyans sonlu olmalıdır (Cauchy gibi sonsuz varyanslı dağılımlarda geçerli değildir).

Akademik Danışmanlık

G*Power Güç Analizi & Örneklem Hesaplama

TRY 749.00

Hizmeti İncele

⭐ Merkezi Limit Teoreminin Önemi

Merkezi limit teoremi, istatistiğin en temel kurallarından biridir. Bunun nedeni:

• Normal dağılıma dayalı olan pek çok teorinin, normal olmayan evrenlerde bile örneklem ortalamaları üzerinden uygulanabilmesini sağlamasıdır.

• Parametrik testlerin (t test, ANOVA, linear regression) gücünü bu teoremden almasıdır.

📘 Sürekli Bir Dağılım Üzerinden Merkezi Limit Teoremi Örneği

ABD’deki emeklilik yaşları üzerine bir çalışma düşünelim.

Evrensel dağılım sola çarpık olabilir ve standart sapması 6 yıl olsun.

Küçük örneklem (n = 5)

Örnek:

68, 73, 70, 62, 63

Ortalama:

68 + 73 + 70 + 62 + 63 / 5 = 67.2

Bu ortalama evreni temsil etmede kesin değildir.

10 küçük örneklem alındığında örneklem ortalamaları örnekleme dağılımını oluşturur.

Bu dağılım hafifçe normale yaklaşsa da hâlâ sol çarpıklık taşır.

Büyük örneklem (n = 50)

50 kişilik örneklem ortalaması:

64.8 yıl

Bu ortalama daha isabetlidir. Çok sayıda 50 kişilik örneklem alındığında dağılım normal şekil alır ve yayılım (standart sapma) azalır.

Örnekleme dağılımı şu şekilde ifade edilir:

📊 Ayrık Bir Dağılım Üzerinde Merkezi Limit Teoremi Örneği

Solaklık olasılığının %10 olduğu varsayılsın.

Solak = 1, sağlak = 0 değerleri kullanılmıştır.

Küçük örneklem (n = 5)

Örnek:

0, 0, 0, 1, 0 → Ortalama = 0.2

10 kez tekrar edildiğinde ortaya çıkan ortalamalar normal değildir çünkü n = 5 küçüktür.

Örneklem büyüklüğü arttıkça

• n = 10 → dağılım normale yaklaşmaya başlar

• n = 20 → daha da simetrik

• n = 30 → normal dağılım görünümü belirginleşir

• n = 100 → örnekleme dağılımı normaldir

Örnekleme dağılımı şu şekilde ifade edilir:

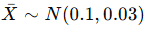
Sıkça Sorulan Sorular: Merkezi Limit Teoremi

Normal dağılım nedir?

Normal dağılım; verilerin tamamen simetrik, çan eğrisi (bell-shaped curve) görünümünde dağıldığı bir yapıdır.Bu dağılımda:

• Değerlerin büyük kısmı merkezin etrafında toplanır,

• Uç değerlerin sıklığı merkeze uzaklaştıkça azalır,

• Ortalama, medyan ve mod birbirine eşittir.

Bu nedenle normal dağılım, birçok istatistiksel testin temel varsayımlarından biridir.

Çarpıklığın (skewness) üç türü nelerdir?

Çarpıklık, dağılımın simetriden ne kadar uzaklaştığını gösterir. Üç ana türü vardır:

• Sağa çarpık (pozitif çarpıklık):Dağılımın sağ kuyruğu soldan daha uzundur. Büyük pozitif uç değerler daha sık görülür.

• Sola çarpık (negatif çarpıklık):Dağılımın sol kuyruğu daha uzundur. Daha düşük uç değerler baskındır.

• Sıfır çarpıklık:Tam simetrik bir dağılımdır. Sol ve sağ taraf birbirinin aynısıdır.

Bu kavramlar, merkezi limit teoreminin örnekleme dağılımındaki dönüşümü anlamak açısından kritik öneme sahiptir.

Araştırmalarda neden örneklemler kullanılır?

Örneklem kullanmanın temel nedenleri şunlardır:

• Pratiklik: Tüm evreni ölçmek çoğu zaman mümkün değildir.

• Maliyet avantajı: Tam sayım yapmak yüksek maliyet gerektirir.

• Zaman verimliliği: Örnekleme ile çok daha hızlı veri elde edilir.

• Yönetilebilirlik: Büyük popülasyonlar yerine küçük örneklemlerle çalışmak analiz sürecini kolaylaştırır.

En önemlisi:Örneklemden elde edilen bulgular, istatistiksel yöntemlerle evren hakkında güvenilir çıkarımlar yapmayı mümkün kılar.