Normal Dağılım: Özellikleri, Kullanım Alanları ve Hesaplama Mantığı

Normal dağılım, istatistik ve bilimsel araştırmalarda en sık karşılaşılan dağılımlardan biridir. Verilerin büyük kısmının bir merkezin etrafında toplandığı, uçlara doğru gidildikçe gözlem sayısının azaldığı karakteristik bir yapıya sahiptir. Grafiğe döküldüğünde simetrik bir çan eğrisi oluştuğu için çan eğrisi veya Gaussian dağılımı olarak da bilinir.

Bu yazıda normal dağılımın temel özelliklerini, neden önemli olduğunu, hangi durumlarda kullanıldığını ve nasıl hesaplandığını adım adım inceleyeceksin.

Normal Dağılımın Neden Önemli Olduğu

Doğal süreçlerde, biyolojik ölçümlerde ve sosyal bilimlerde gözlenen pek çok değişken normal veya normale yakın dağılım gösterir.

Örneğin:

• Boy uzunluğu

• Doğum ağırlığı

• Okuma becerisi

• Job satisfaction (iş doyumu)

• Standart test skorları (SAT gibi)

Bu nedenle çok sayıda parametrik istatistiksel test, popülasyonun normal dağıldığını varsayarak çalışır. Verilerin normal dağılıma uygun olup olmadığı araştırmacının hangi istatistiksel araçları kullanabileceğini doğrudan belirler.

Normal Dağılımın Temel Özellikleri

Normal dağılımın kolayca fark edilen bazı matematiksel özellikleri vardır:

1. Ortalama, Medyan ve Mod Aynıdır

Merkezde tek bir tepe noktası bulunur. Bu tepede üç değer birleşir:

• Ortalama (mean)

• Medyan (median)

• Mod (mode)

Bu nedenle normal dağılım tek modlu ve tamamen simetriktir.

2. Dağılım Ortalama Etrafında Simetriktir

Ortalamanın solunda kalan değerlerin oranı ile sağında kalan değerlerin oranı eşittir.

Yani:

• Verilerin %50’si ortalamanın altında,

• %50’si ortalamanın üzerindedir.

Bu simetri, normal dağılımı modellemeyi ve çözümleri kolaylaştırır.

3. Dağılım İki Parametre ile Tanımlanır

Bir normal dağılımı tanımlamak için iki bilgi yeterlidir:

• Ortalama (µ) → Eğrinin merkezini belirler.

• Standart sapma (σ) → Eğrinin genişliğini belirler.

Standart sapma küçükse eğri dar ve sivri, büyükse geniş ve yayvandır.

Ortalama ve Standart Sapmanın Eğriyi Nasıl Değiştirdiği

Ortalama (µ) değişirse:

• Eğri sağa veya sola kayar.

• Dağılımın yüksekliği ve şekli değişmez.

Standart sapma (σ) değişirse:

• Küçük σ → Dar, yüksek bir eğri.

• Büyük σ → Yayvan, geniş bir eğri.

Ampirik Kural (68–95–99.7 Kuralı)

Normal dağılımı anlamanın en hızlı yolu budur:

• %68 → Değerler ortalamanın ±1 standart sapma içinde.

• %95 → Değerler ortalamanın ±2 standart sapma içinde.

• %99.7 → Değerler ortalamanın ±3 standart sapma içinde.

Örnek

Bir dersin ortalama SAT puanı 1150, standart sapması 150 ise:

• %68 öğrenci 1000 – 1300 arasında puan alır.

• %95 öğrenci 850 – 1450 arasında.

• %99.7 öğrenci 700 – 1600 arasında.

Bu alanlar, grafik üzerinde çan eğrisi altında belirli bölgeleri temsil eder.

Merkezi Limit Teoremi ile Normal Dağılımın İlişkisi

Merkezi Limit Teoremi (CLT), istatistiğin temel taşlarından biridir ve aşağıdaki iki kilit mesajı verir:

1. Büyük örneklemlerde örneklem ortalamaları normal dağılır.

Popülasyon dağılımı çarpık, düzensiz hatta bimodal bile olsa; örneklem büyüklüğü arttıkça örneklem ortalaması normal dağılıma yaklaşır.

2. Örneklem sayısı arttıkça örneklem ortalaması popülasyon ortalamasına yaklaşır.

Bu, tahmin yapmayı mümkün kılar ve t-test gibi parametrik yöntemlerin güvenilirliğini sağlar.

Genellikle n ≥ 30 olduğunda örneklem ortalamaları yaklaşık normal kabul edilir.

Normal Eğrinin Matematiksel Formülü

Normal dağılımın probability density function (PDF) formülü şöyledir:

Bu fonksiyon:

• Eğrinin şeklini belirler,

• Olasılıkların eğri altındaki alan aracılığıyla hesaplanmasını sağlar,

• Dağılımın toplam alanını 1’e eşitler.

Standart Normal Dağılım (Z-Dağılımı)

Standart normal dağılım, normal dağılımın özel bir halidir:

• Ortalama = 0

• Standart sapma = 1

Normal dağılım değerlerinin z-skorlarına dönüştürülmesi karşılaştırmayı kolaylaştırır.

Z-skoru formülü

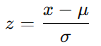
Bu skor, bir gözlemin ortalamadan kaç standart sapma uzakta olduğunu gösterir.

Z-Dağılımı ile Olasılık Hesaplama

Bir değerin belirli bir aralıkta olma olasılığı z-skoru kullanılarak bulunur.

Örnek

SAT puanı 1380’in olasılığını bulalım:

Z-tablosu:

• z = 1.53 → p = 0.937

Bu, 1380’in altında değer alma olasılığıdır.

Üst tarafı istediğimiz için:

P(x > 1380) = 1 − 0.937 = 0.063

Yani öğrencilerin yalnızca %6.3’ü 1380’in üzerinde puan alır.

Akademik Danışmanlık

İntihal Düzenleme & Düzeltme

Hizmeti İncele

Normal Dağılım Hangi Durumlarda Kullanılır?

• Bireylerin test skorlarını yorumlama

• Kalite kontrol süreçlerinde dağılım tahmini

• Zaman, ölçüm, ağırlık gibi sürekli değişkenlerin analizi

• Parametrik testlerin uygulanabilirliğini kontrol etme

• Olasılık hesaplama ve tahmin