Sabit Değerden Fark Korelasyon Testinde Örneklem Büyüklüğü ve Güç Analizi

Korelasyon analizlerinde, popülasyondaki gerçek ilişkinin önceden belirlenmiş bir sabit değerden farklılaşıp farklılaşmadığını test etmek sıkça gerekli olur.

G*Power’ın “Exact: Correlation Bivariate normal model” prosedürü, bu tür tek örneklem testlerinde hem küçük hem de büyük örneklemler için doğru güç analizi sunar.

Aşağıda, konuyu kavramanızı kolaylaştıracak alt başlıklar eşliğinde temel terimler ve izlenecek adımlar özetlenmiştir.

Testin Amacı ve Hipotez Yapısı

Bu test, iki değişken arasındaki popülasyon korelasyonunu ρ₀ sabit değeri ile karşılaştırır.

• H₀ (Null): ρ − ρ₀ = 0 (fark yok)

• H₁ (Alternative): ρ − ρ₀ ≠ 0 (fark var)

İki kuyruklu analiz (“two tails”) sapmanın yönüne dair ön bilgi yokken, tek kuyruklu (“one tail”) belirli yönde artış ya da azalma beklendiğinde tercih edilir.

Etki Büyüklüğü (Effect Size)

Etki büyüklüğü, ρ ile ρ₀ arasındaki fark olarak tanımlanır: Δρ = ρ − ρ₀.

• Geçerlilik sınırı: −1 + ε < ρ < 1 − ε, ε = 10⁻⁶

• A priori hesaplamalarda |Δρ| > ε olmalıdır.

• Cohen’e göre ρ₀ = 0 özelinde:

  • Küçük etki: 0,10

  • Orta etki: 0,30

  • Büyük etki: 0,50

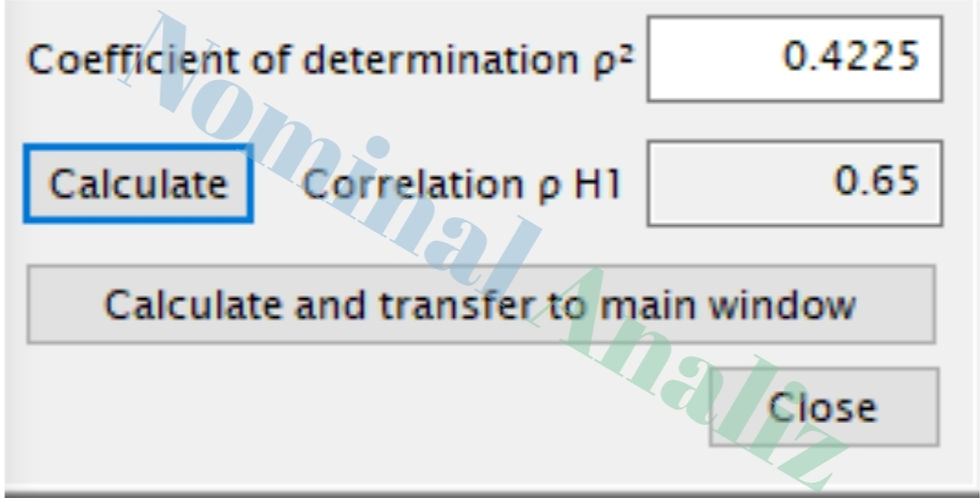
“Determine” butonuyla, elinizdeki r² değerinden de ρ hesaplayabilirsiniz.

Arayüzde Doğru Seçimler

G*Power penceresinde aşağıdakileri ayarlayın:

• Test family: Exact

• Statistical test: Correlation: Bivariate normal model

• Type of power analysis: A priori: Compute required sample size – given α, power, and effect size

Eğer “Difference from constant” doğrudan görünmüyorsa, “Bivariate normal model” altındaki korelasyon seçeneklerinden yararlanabilirsiniz.

Hesaplama Seçenekleri (Options)

“Options” penceresinde:

• Use exact distribution if N < X seçeneği işaretli kalsın (örneğin X = 10000).

• Büyük örneklemler için Fisher Z yaklaşımını tercih etmek isterseniz “Use large sample approximation (Fisher Z)” seçeneğini aktif edebilirsiniz.

Hangi prosedürün kullanıldığını, protokol sekmesindeki “Option” alanından ve grafiklerdeki “r” veya “z” etiketlerinden anlayabilirsiniz.

Bu kavramları pekiştirmek için gerçek bir veri seti üzerinde “Sabit Değerden Fark Korelasyon Testi”ni uygulayacağız. Bir sonraki çalışmamızda adım adım örnek bir senaryo üzerinden analiz yapacağız ve elde edilen sonuçları yorumlayacağız.

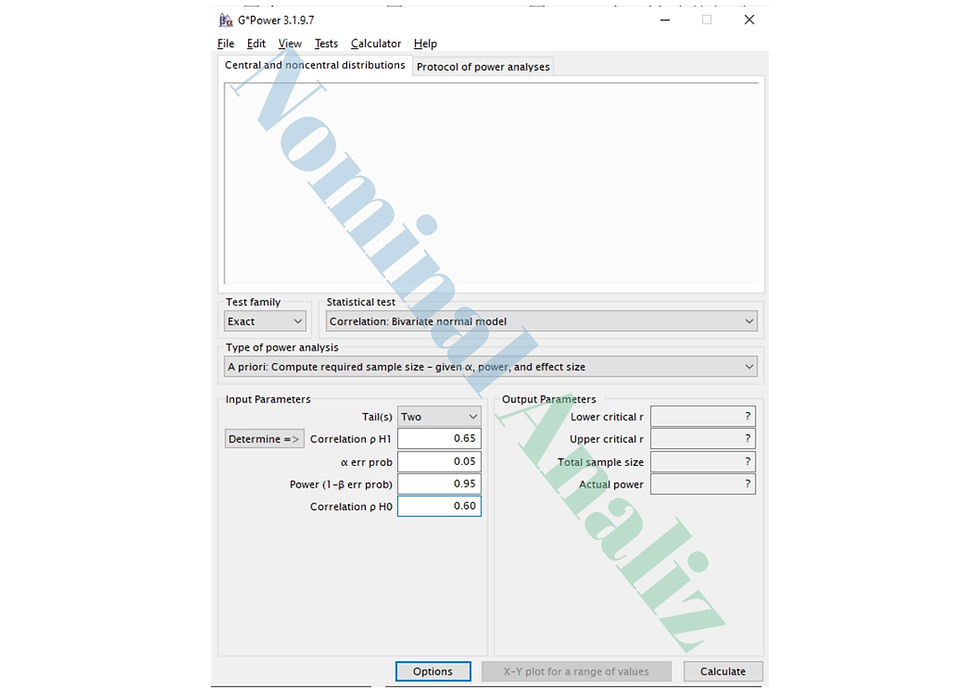
Girdi Parametrelerinin Tanımı

İki kuyruklu A priori analize yönelik örnek girdi:

• Tail(s): Two

• Correlation ρ H₁: 0,65

• Correlation ρ H₀: 0,60

• α err prob: 0,05

• Power (1 − β err prob): 0,95

Bu değerleri girip “Calculate” dediğinizde G*Power, alt/üst kritik r sınırlarını ve gereken örneklem büyüklüğünü hesaplar.

Sonuçların Yorumlanması

Girdiğiniz değerler (ρ₀ = 0,60; ρ₁ = 0,65; α = 0,05; güç = 0,95; two tails; exact dağılım) ile elde edilen çıktılar şöyle:

• Alt kritik r: 0,570748

• Üst kritik r: 0,627919

• Gerekli toplam örneklem büyüklüğü (N): 1928

• Gerçekleşen güç: 0,950028

G*Power çıktısı size şu bilgileri verir:

• Lower critical r, Upper critical r: Anlamlı kabul edilecek korelasyon aralığı dışındaki değerler H₀’ı reddetmenizi sağlar.

• Total sample size: Hedef güç ve etki büyüklüğü için gereken katılımcı sayısı.

• Actual power: Girilen N değeriyle elde edilen gerçek güç.

Örneğin ρ₀=0,60’dan ρ₁=0,65’e yükselişi test etmek için yaklaşık 1928 denek gereklidir ve bu koşullarda güç ≈ 0,95 olur.

Yorum: Bu ayarlarla, örneklemden elde edeceğiniz korelasyon katsayısı r

• 0,571’in altındaysa veya

• 0,628’in üstündeyse

%95 güvenle ρ = 0,60 sabit değerinden anlamlı olarak farklı olduğunu (H₀ reddedildiğini) söyler. Ayrıca bu güce ulaşmak için yaklaşık 1928 katılımcı gereklidir.