G*Power ile İki Bağımlı Ortalama (Eşleştirilmiş Gruplar) t-Testi ve Güç Analizi

Testin Temeli

İki bağımlı ortalamanın farkını test eden eşleştirilmiş t-testi (paired samples t-test), aynı bireylerin iki ölçümünden (ön-test/son-test gibi) veya eşleştirilmiş iki farklı gruptan elde edilen değerler arasındaki ortalama farkın istatistiksel olarak anlamlı olup olmadığını test eder.

• H₀ (Null Hipotezi): μₓ – μᵧ = 0 (iki ölçümün ortalamaları eşittir)

• H₁ (Alternatif Hipotez): μₓ – μᵧ ≠ 0 (iki ölçüm arasında anlamlı fark vardır)

Bu testin avantajı, her bireyin veya eşleştirilmiş grubun kendi “kontrolü” gibi davranmasıdır. Böylece bireysel varyanslar azaltılır ve testin gücü artar. Eğer farkın yönü önceden bilinmiyorsa iki yönlü test, yön netse tek yönlü test tercih edilir.

Etki Büyüklüğü (dz)

İki bağımlı ortalama arasındaki fark Cohen’in dz değeri ile ifade edilir.

• Küçük etki: dz ≈ 0.2

• Orta etki: dz ≈ 0.5

• Büyük etki: dz ≥ 0.8

dz değeri, iki ölçümün ortalama farkının standart sapmasına bölünmesiyle bulunur. Bu değeri G*Power’da “Determine” ekranında ortalamalar, standart sapmalar ve gruplar arası korelasyon girilerek hesaplayabilirsiniz. Korelasyon, eşleştirmenin test gücüne katkısını doğrudan yansıtır: korelasyon ne kadar yüksekse, aynı örneklemle o kadar yüksek güç elde edilir.

Bakış Açısı Genişleten Notlar

• Eşleştirilmiş Tasarım Avantajı: Bağımsız iki gruptan ziyade eşleştirilmiş gruplarla çalışmak, bireysel farklılıkları kontrol ettiği için genellikle daha az örneklemle aynı güce ulaşmayı sağlar.

• Korelasyonun Önemi: Eşleştirilmiş verilerde gruplar arası korelasyon yükseldikçe standart hata düşer, dolayısıyla test gücü artar.

• Tek/Çift Yön Seçimi: Tek yönlü test gücü artırır ancak yön hipotezde önceden belirtilmelidir.

Uygulamalı Çalışma: Cohen (1969) Örneği (G*Power Analizi)

Senaryo: İki öğretim yönteminin cebir başarısı üzerindeki etkisi, IQ’ya göre eşleştirilmiş 50 çift (toplam 100 öğrenci) üzerinde test ediliyor. Etki büyüklüğü d=0.4, gruplar arası korelasyon r=0.55 olarak varsayılıyor. Bu parametrelerle G*Power kullanılarak post hoc güç analizi yapılıyor.

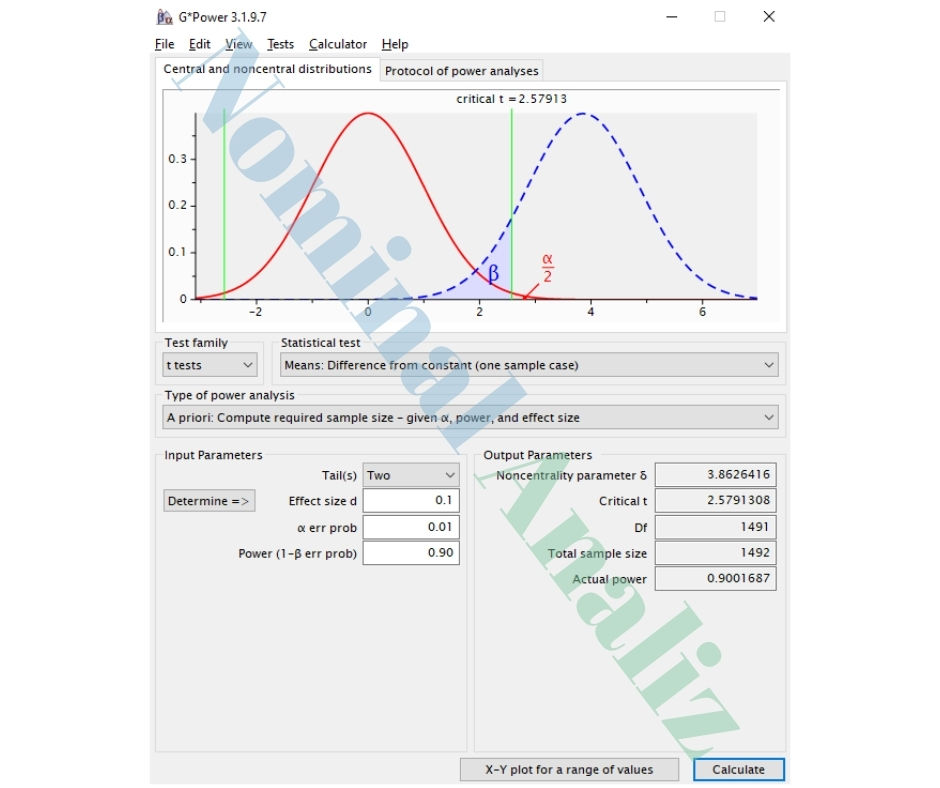
Girdi Parametreleri:

• Analiz Türü: Post hoc

• Tail(s): Two

• Effect size dz: 0.421637 (G*Power’ın “Determine” ekranında korelasyon girilerek elde edilen değer)

• α err prob: 0.05

• Total sample size: 50

Çıktı Parametreleri (G*Power):

• Noncentrality parameter δ: 2.981424

• Critical t: 2.009575

• df: 49

• Power (1–β err prob): 0.832114

Yorum

• Güç %83,2: Bu parametrelerle testin gerçek bir farkı saptama olasılığı %83’tür. Cohen’in tablosundaki değere (0.84) çok yakındır.

• Noncentrality Parameter (δ=2.98): Etki büyüklüğü, korelasyon ve örneklem büyüklüğünün birleşik göstergesidir; δ yükseldikçe güç de artar.

• Critical t=2.0096: α=0.05 çift yönlü test için kritik t-değeri; test istatistiği bu değeri aşarsa H₀ reddedilir.

• Df=49: 50 eşleşmiş gözlemden gelen serbestlik derecesini gösterir.

Bağımsız İki Grup ile Karşılaştırma: Aynı etki büyüklüğüyle (d=0.4) bağımsız iki grup tasarımında güç sadece %50 civarında olacaktı. Yani eşleştirme, örneklem ihtiyacını yarıdan fazla azaltarak gücü artırmıştır.

Pratik Değerlendirme

Bu örnek şunu gösteriyor:

• Korelasyon yüksek ve veriler eşleştirilmiş olduğunda daha az sayıda kişiyle aynı güce ulaşılabilir.

• Test tasarımında eşleştirme düşünülerek kaynak kullanımı ve zaman yönetimi optimize edilebilir.

• Tek/çift yön seçimi ve alfa seviyesi (ör. 0.05 yerine 0.01) test gücü ve örneklem büyüklüğü üzerinde doğrudan etkilidir.