G*Power ile Tek Örneklem t-Testi (Means – Difference from Constant)

Testin Temeli

Tek örneklem t-testi, bir popülasyon ortalamasının belirli bir sabit değere (μ₀) eşit olup olmadığını test eden parametrik bir yöntemdir. Bu test, küçük veya orta büyüklükte örneklemlerde bile sıklıkla kullanılır ve popülasyonun standart sapması bilinmediği durumlarda tahmini standart sapmayı kullanır.

• H₀ (Null Hipotezi): μ – μ₀ = 0 (Popülasyon ortalaması sabite eşit)

• H₁ (Alternatif Hipotez): μ – μ₀ ≠ 0 (Popülasyon ortalaması sabitten farklı)

Varsayımlar:

• Veri normal dağılmalı.

• Standart sapma bilinmiyorsa örneklemden tahmin edilmeli.

• Örneklem rastgele seçilmiş olmalı.

Eğer farkın yönü önceden tahmin edilemiyorsa iki yönlü test (two-tailed) tercih edilir. Eğer yön biliniyorsa tek yönlü test (one-tailed) güç avantajı sağlar.

Etki Büyüklüğü (Cohen’s d)

Bu testte etki büyüklüğü, ortalama farkın standart sapmaya bölünmesiyle bulunur:

d = (μ – μ₀) / σ

Bu değer, popülasyon ortalamasının sabitten kaç standart sapma uzakta olduğunu gösterir.

Cohen’in standartlarına göre:

• Küçük Etki: d = 0.2

• Orta Etki: d = 0.5

• Büyük Etki: d = 0.8

G*Power’ın Determine butonu ile μ, μ₀ ve σ girildiğinde d otomatik hesaplanabilir.

Bakış Açısı Genişleten Notlar

• Örneklem ve Etki Büyüklüğü İlişkisi: Küçük bir etkiyi görebilmek için büyük bir örneklem gerekir; güçlü bir etki için küçük örneklem yeterli olabilir.

• Tek/Çift Yönlü Test Etkisi: Tek yönlü test daha yüksek güç verir; ancak hipotezin yönü net bilinmeli.

• Planlama ve Pilot Çalışmalar: Tahmini d değeri literatürden veya pilot çalışmadan alınabilir.

Uygulamalı Çalışma: Tek Örneklem t-Testi G*Power Analizi

Senaryo: Popülasyon ortalamasının μ₀=10 olduğu varsayılıyor; yeni ölçümde μ=15. Tahmini σ=8. Yalnızca artış yönüyle ilgilenildiği için tek yönlü test seçildi.

Girdi Parametreleri:

• Analiz Türü: A priori

• Tail(s): One

• Effect size d: 0.625

• α err prob: 0.05

• Power (1-β err prob): 0.95

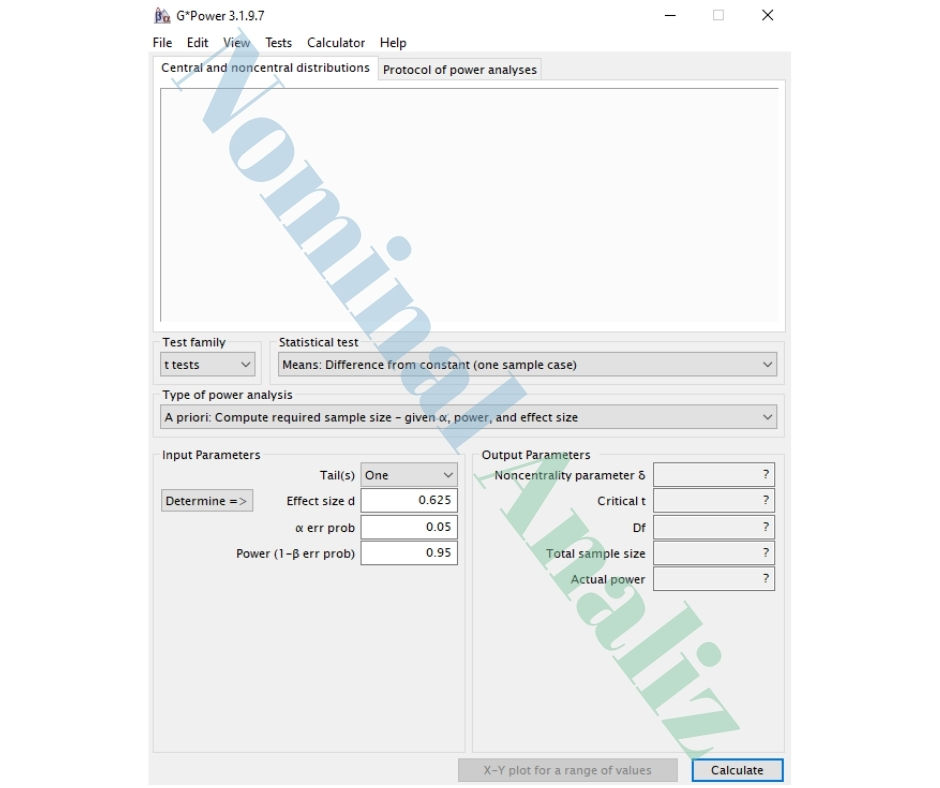
G*Power Çıktısı:

• Noncentrality parameter δ: 3.423266

• Critical t: 1.699127

• Df: 29

• Total sample size: 30

• Actual power: 0.955144

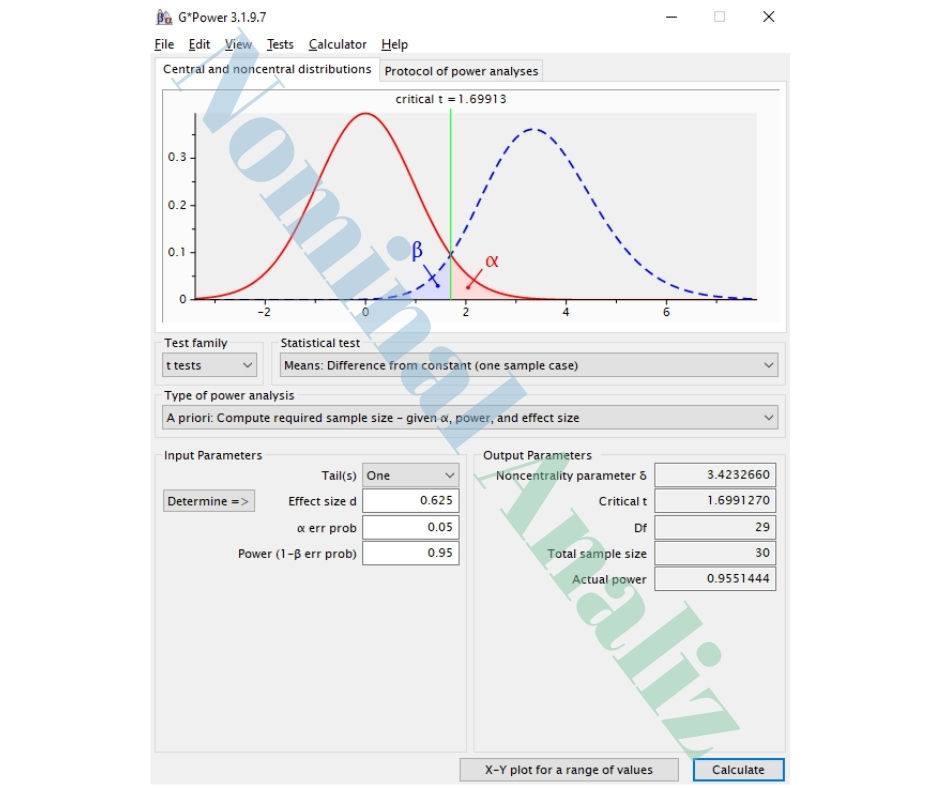
Yorum:

• Güç %95,5: Bu, çalışmanızın gerçek bir farkı %95 olasılıkla saptayabileceğini gösterir.

• Noncentrality parameter δ=3.42: Etki büyüklüğü ve örneklem büyüklüğünün birleşik etkisi. δ ne kadar büyükse güç o kadar yüksek olur.

• Critical t=1.6991: α=0.05 tek yönlü test için kritik t-değeri; test istatistiği bu değeri aşarsa H₀ reddedilir.

• Df=29: Örneklem büyüklüğünün (N=30) yansımasıdır.

Değerlendirme

Bu örnek, tek örneklem t-testinde d=0.625 gibi orta büyüklükte bir etki için 30 kişilik örneklemle %95’in üzerinde güç elde edilebildiğini göstermektedir. Daha küçük d değerlerinde aynı güce ulaşmak için örneklem büyüklüğünün artması gerekecektir. Bu analiz, araştırma tasarımınızı planlarken örneklem büyüklüğünü ve test yönünü stratejik seçmenin önemini net biçimde ortaya koyar.

Uygulamalı Çalışma 2: Çok Küçük Etkiyi Yakalamak (d=0.10)

Amaç: Sabitten çok küçük bir sapmayı güvenilir biçimde saptayacak örneklem büyüklüğünü belirlemek.

Girdi Parametreleri (G*Power)

• Type of power analysis: A priori

• Tail(s): Two

• Effect size d: 0.10

• α err prob: 0.01

• Power (1–β err prob): 0.90

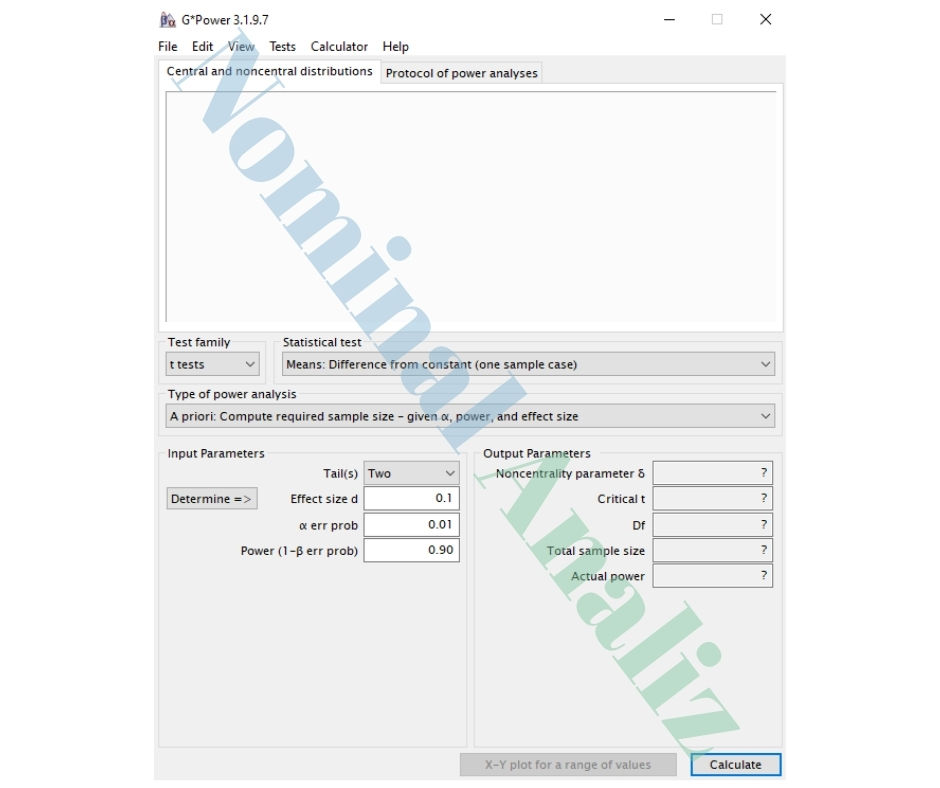
G*Power Çıktıları

• Noncentrality parameter δ: 3.862642

• Critical t: 2.579131

• df: 1491

• Total sample size: 1492

• Actual power: 0.900169

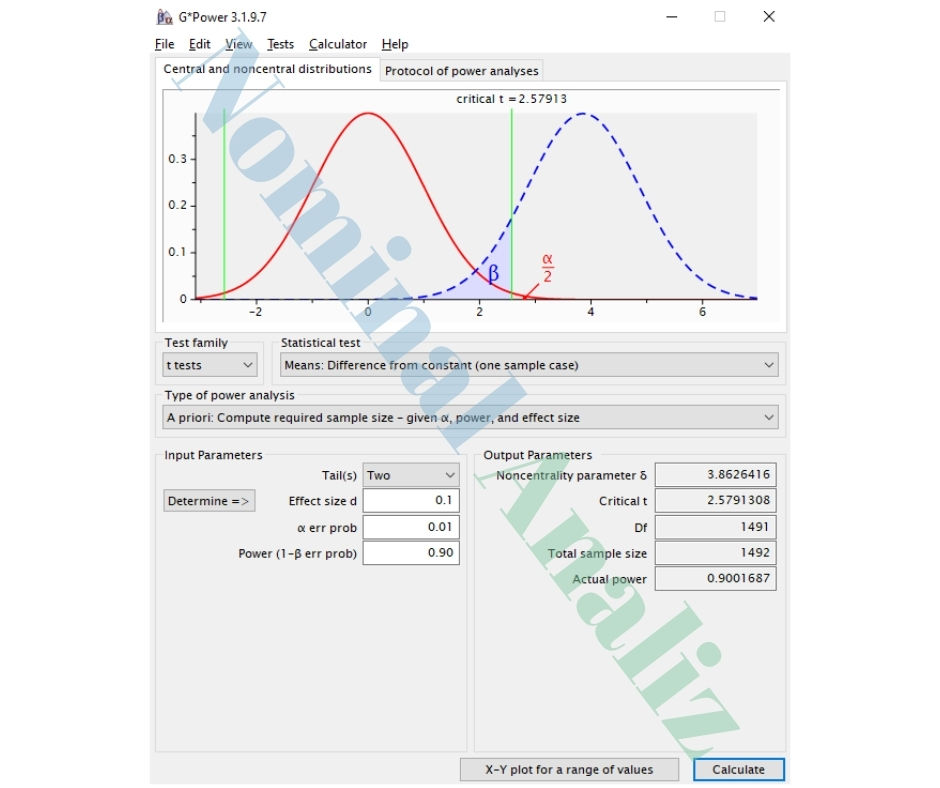
Yorum

• Örneklem gereksinimi çok yüksek: d=0.10 düzeyindeki çok küçük bir farkın %90 güç ve %1 tip-I hata ile yakalanması için 1492 kişi gerekiyor. Bu, küçük etkilerin güvenilir tespiti için geniş örnekleme ihtiyaç duyulduğunu gösterir.

• İki yönlü ve sıkı alfa tercihi maliyetli: Two-tailed test ve 0.01 alfa, eşiği yükseltir; güç hedefi sabitken örneklem büyür. Yönün önceden bilindiği ve etik olarak savunulabildiği durumlarda tek yönlü kurgu örneklem talebini azaltır.

• Planlama önerisi:

  • Literatürden veya pilot çalışmadan daha gerçekçi bir d tahmini alın.

  • Kaynak kısıtı varsa hedef gücü 0.80’e çekmek, alfa=0.05’e dönmek ya da ölçümü daha duyarlı hale getirip d’yi büyütmek seçenekleri değerlendirilmelidir.

• Sonuç: Parametre seçimi (alfa, yön, güç hedefi) ile etki büyüklüğü birlikte düşünüldüğünde, bu senaryoda küçük farkları yakalamak için büyük ölçekli bir çalışma gerekir. Bu analiz, tasarım kararlarının örneklem büyüklüğü üzerindeki etkisini açık biçimde ortaya koyar.

Karşılaştırmalı Tablo Üzerinden Tek Örneklem t-Testi

Parametre / Senaryo	Uygulamalı Çalışma 1 Normal Dağılım, d=0.625	Uygulamalı Çalışma 2 Çok Küçük Etki, d=0.10
Analiz Türü	A priori	A priori
Tail(s)	One (tek yönlü)	Two (çift yönlü)
Parent Distribution	Normal	Normal
Effect Size d	0.625	0.10
α err prob	0.05	0.01
Power (1–β err prob)	0.95	0.90
Total Sample Size	30	1492
Noncentrality parameter δ	3.423266	3.862642
Critical t	1.699127	2.579131
Df (serbestlik derecesi)	29	1491
Actual Power	0.955144 (%95,5)	0.900169 (%90,0)

Değerlendirme

Etki Büyüklüğü ve Örneklem İlişkisi:– İlk senaryoda orta büyüklükte bir etki (d=0.625) sadece 30 kişilik örneklem ile %95’in üzerinde güç sağladı.– İkinci senaryoda çok küçük etki (d=0.10) için %90 güç elde etmek 1492 kişilik örneklem gerektirdi.

Test Yönü ve Alfa Seviyesi:– Tek yönlü test (α=0.05) güç avantajı sağladı; çift yönlü ve daha sıkı alfa (α=0.01) örneklem gereksinimini dramatik artırdı.

Noncentrality Parameter (δ):– δ ikinci senaryoda yüksek görünse de bu, büyük örneklemle elde edilmiştir. δ’nin yüksek olması, istatistiksel gücün artmasına katkı sağlar.

Pratik Sonuç: Bu kıyaslama, etki büyüklüğü, test yönü, alfa seviyesi ve örneklem büyüklüğü gibi parametrelerin birlikte ele alınmasının önemini açık biçimde gösterir. Küçük etkilerin tespiti için geniş örnekleme gerek varken, daha büyük etkiler daha küçük örneklemlerle güvenilir şekilde bulunabilir. Araştırma tasarımında bu dengeler dikkate alındığında hem kaynak hem de zaman yönetimi optimize edilir.