Normallik Analizine Dayalı Uygulamalı Çalışma ve SPSS ile Tek Örneklem T-Testi: Üniversite Öğrencilerinde Uyku Süresi, Sınav Başarısı ve Yaşam Memnuniyeti (n=90) İlişkisi

Tek Örneklem T Testi öncesinde ilk ve en önemli adım, veri setinizin normal dağılım gösterip göstermediğini analiz etmektir. Çünkü Tek Örneklem T Testi, parametrik bir yöntem olup, uygulanabilmesi için analiz edilen değişkenin normal dağılıma uygun olması gerekmektedir.

Veri seti şu şekildedir:

Veri setinin variable view ekranında değişken tanımlaması ise şu şekildedir:

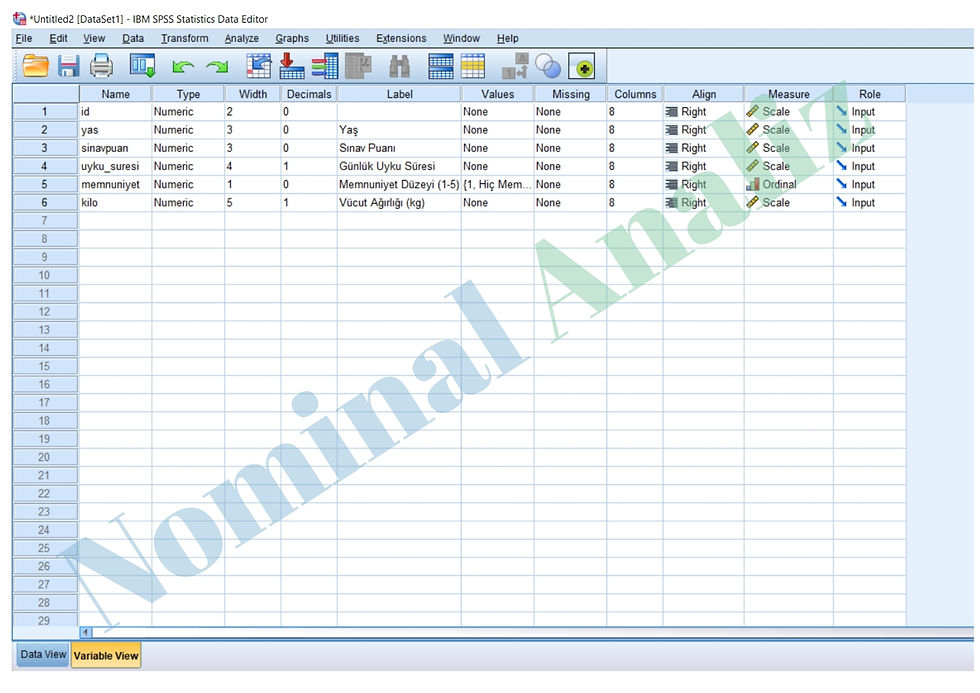
Veri setinde incelenen tüm değişkenler (“Günlük Uyku Süresi”, “Vücut Ağırlığı (kg)”, “Sınav Puanı”), hem istatistiksel testler (Kolmogorov-Smirnov, Shapiro-Wilk) hem de histogram, Q-Q plot, stem-leaf ve boxplot gibi grafiksel analizler açısından normallik varsayımını karşılamaktadır. Bu sonuçlara göre, her bir değişken için parametrik istatistiksel analizler güvenle uygulanabilir. Araştırmanın sonraki adımlarında t-testi, ANOVA gibi parametrik yöntemleri kullanmak için normallik yönünden herhangi bir kısıtlama yoktur.

SPSS ile yapılan kapsamlı normallik analizi raporunun detaylarını okumak için aşağıdaki bağlantıya tıklayabilirsiniz.

Uygulamalı Normallik Analizi Çalışmasını İncelemek için Tıklayın

Tek Örneklem T Testi Nedir? Nelere Dikkat Edilir? (Kısa Teorik Bilgi)

Tek Örneklem T Testi, bir örneklemden elde edilen ortalamanın, belirlenen bir sabit değere (popülasyon ortalaması gibi) anlamlı düzeyde farklı olup olmadığını test eden parametrik bir istatistiksel analizdir. Bu testin uygulanabilmesi için:

• Verilerin normal dağılıma uygun olması gerekir (normallik analizi ile sağlanır).

• Veriler sürekli ve nicel olmalıdır.

• Test sonucunda elde edilen p değeri (Sig.), genellikle 0,05’ten küçükse, örneklem ortalamasının test edilen değerden anlamlı biçimde farklı olduğu kabul edilir.

Sonuçların doğru yorumlanabilmesi için, normallik varsayımına dikkat edilmeli ve istatistiksel anlamlılık p-değeri üzerinden değerlendirilmelidir.

SPSS’te Tek Örneklem T Testi Nasıl Yapılır?

1. Veri Girişi

• Verilerinizi SPSS’e aktarın veya “Variable View” sekmesinde değişkenlerinizi tanımlayın. “Data View” ekranında veri girişini yapın.

2. Menüden Gerekli Komutu Seçin

• Üst menüden Analyze → Compare Means → One-Sample T Test… yolunu izleyin.

3. Test Edilecek Değişkeni Seçin

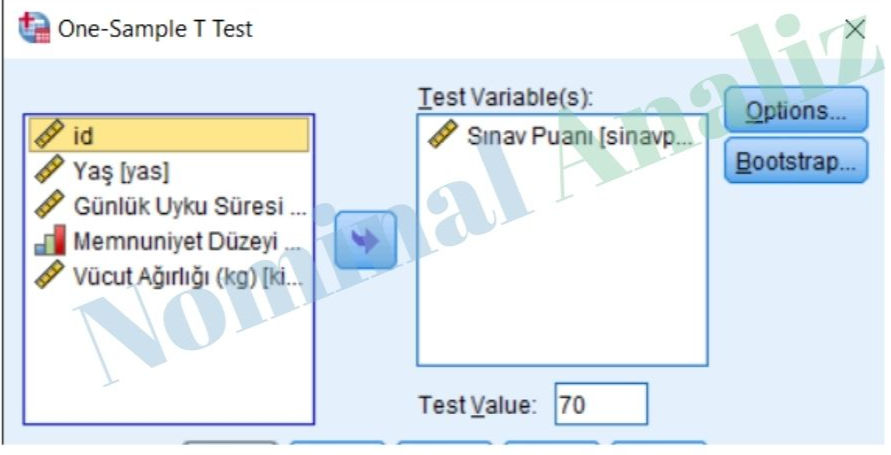
• Açılan pencerede, test yapmak istediğiniz değişkeni Test Variable(s) kutusuna aktarın (örneğin: “sinavpuan”, “uyku_suresi”, “kilo” gibi).

4. Test Değerini Girin

• Test Value kutusuna, karşılaştırmak istediğiniz teorik/popülasyon ortalamasını yazın.(Örneğin: Bir sınavda beklenen ortalama puan 70 ise, “70” yazılır.)

5. Testi Başlat

• OK butonuna tıklayarak testi başlatın.

6. SPSS Çıktısını Yorumlayın

• SPSS çıktı penceresinde:

  • “One-Sample Statistics” tablosunda örneklem ortalaması, standart sapma ve örneklem büyüklığını görebilirsiniz.

  • “One-Sample Test” tablosunda t, p (Sig. (2-tailed)), mean difference ve güven aralığı değerleri yer alır.

Kısa Yorumlama İpuçları:

• p < 0,05 ise: Örneklem ortalaması ile test edilen ortalama arasında istatistiksel olarak anlamlı bir fark vardır.

• p > 0,05 ise: Örneklem ortalaması ile test edilen ortalama arasında anlamlı bir fark yoktur.

Bu örnek çalışma için test edilen değişken "Sınav Puanı"'dır. "Test Value" kısmına "70" yazılmış ve analiz için incelemeye alınmıştır.

One-Sample Statistics Tablosu:

One-Sample T-Test (Tek Örneklem t Testi) SPSS Çıktısının Yorumlanması

1. One-Sample Statistics Tablosu

Bu tablo, örneklemimize (90 kişi) ait temel tanımlayıcı istatistikleri gösterir:

• Mean (Ortalama): 72,36Örneklemdeki sınav puanlarının ortalaması.

• N (Örneklem Büyüklüğü): 90Analize dahil edilen kişi sayısı.

• Std. Deviation (Standart Sapma): 4,356Puanların ortalamadan ne kadar sapma gösterdiğini ifade eder.

• Std. Error Mean (Standart Hata): 0,459Ortalama puanın tahmini hata payı. Büyük örneklemlerde küçük olur.

2. One-Sample Test Tablosu

Bu bölümde, örneklem ortalaması ile belirlediğimiz test değeri (bu analizde “70”) arasında anlamlı bir fark olup olmadığı test edilmiştir.

• Test Value = 70: Buradaki "70", örneklemimizdeki sınav puanlarının karşılaştırıldığı referans (popülasyon) ortalamasıdır.

• t = 5,130: Hesaplanan t değeri; örneklem ortalamasının test değerinden ne kadar uzaklaştığını gösterir.

• df = 89: Serbestlik derecesi; örneklem büyüklüğü eksi bir (N-1).

• Sig. (2-tailed) = 0,000: p değeri. Eğer bu değer 0,05’ten küçükse, fark istatistiksel olarak anlamlıdır.

• Mean Difference = 2,356: Örneklem ortalaması ile test değeri (70) arasındaki fark.

• 95% Confidence Interval of the Difference (Güven Aralığı): [1,44 – 3,27]Gerçek ortalama farkının %95 olasılıkla bu aralıkta olduğu anlamına gelir.

SPSS Çıktısının Anlamı ve Sonuç Yorumu

• p değeri (Sig.) 0,000, yani p < 0,05 olduğundan örneklemimizin sınav puanı ortalaması (72,36) ile popülasyon/test ortalaması (70) arasında istatistiksel olarak anlamlı bir fark vardır.

• Örneklemimizdeki öğrencilerin sınav puanı ortalaması, popülasyon ortalamasından (70) anlamlı düzeyde daha yüksektir.

Kullanıcıya Yönelik Açıklama:

Bu analiz sayesinde, elimizdeki 90 kişilik üniversite öğrencisi örnekleminde sınav puanı ortalamasının genel kabul gören ortalamanın (70) üstünde ve anlamlı bir farkla yüksek olduğunu söyleyebiliriz. Başka bir deyişle, öğrencilerimiz genel ortalamanın üzerinde bir sınav başarısı göstermektedir.