Normallik Analizi Uygulamalı Çalışma ve Yorumlama - Üniversite Öğrencilerinde Uyku Süresi, Sınav Başarısı ve Yaşam Memnuniyeti İlişkisi (90 Kişilik Örneklem Büyüklüğü)

Nominal Analiz
20 Tem
8 dakikada okunur

Normallik Analizi Nedir? (Özet Bilgi)

Normallik analizi, bir veri setinin istatistiksel olarak normal dağılıma (çan eğrisi şeklinde, simetrik dağılım) uyup uymadığını kontrol etme işlemidir.

Bir Veri Setinin Normal Dağılıma Uyup Uymadığını Gösteren Kriterler:

Ortalama, Medyan ve Mod: Değerler birbirine yakınsa normal dağılım ihtimali yüksektir.
Çarpıklık (Skewness) ve Basıklık (Kurtosis) Katsayıları:
- Skewness ve Kurtosis genellikle -1 ile +1 aralığındaysa normal dağılım kabul edilir.
Histogram ve Q-Q Plot:
- Histogramda çan eğrisi şekli,
- Q-Q Plot’ta noktalar 45°’lik çizgiye yakınsa normallik sağlanır.
Normallik Testleri:
- Kolmogorov-Smirnov (n≥30) ve Shapiro-Wilk (n<30) testlerinde
  - p > 0,05 ise: Normal dağılım var
  - p < 0,05 ise: Normal dağılım yok

Özet: Veri simetrik, ortalama-medyan-mod birbirine yakın, çarpıklık/basıklık kabul sınırında ve normallik testi p>0,05 ise veri normal dağılıma uygundur.

Şimdi uygulamaya geçelim.

Aşağıdaki görsel "Üniversite Öğrencilerinde Uyku Süresi, Sınav Başarısı ve Yaşam Memnuniyeti İlişkisi" konulu veri setine aittir.

Üniversite Öğrencilerinde Uyku Süresi, Sınav Başarısı ve Yaşam Memnuniyeti İlişkisi Normallik Analizi Veri Seti

Aşağıdaki görsel ise değişkenlerin Variable View ekranında ayarlanması ve tanımlanmış haline aittir.

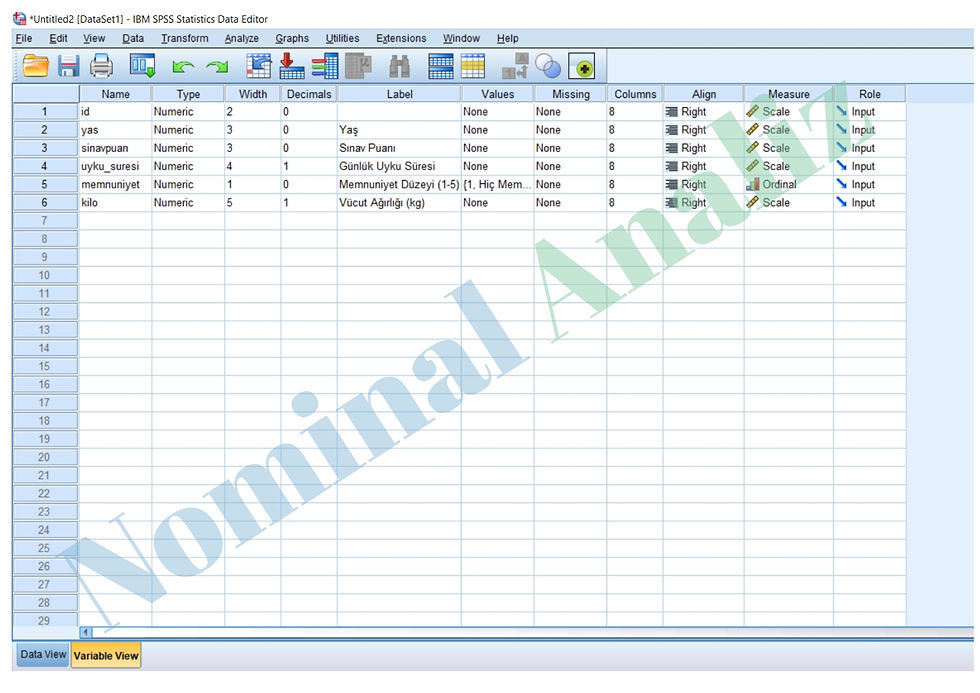
Üniversite Öğrencilerinde Uyku Süresi, Sınav Başarısı ve Yaşam Memnuniyeti İlişkisi Normallik Analizi Veri Setinin Variable View Ekranında Düzenlenmesi ve Tanımlanması

SPSS’te Normallik Analizi Yapma Adımları

1. Verinizi Girin

Değişkenlerinizi (örn. sinavpuan, uyku_suresi, kilo, vb.) Data View sekmesine girin.
Değişken isimlerini ve ayarlarını Variable View kısmında kontrol edin.

2. Normallik Testi için Menüyü Açın

Üst menüden Analyze → Descriptive Statistics → Explore... seçin.

3. Değişkenleri Seçin

Dependent List kısmına normalliğini test etmek istediğiniz nicel (sayısal) değişkenleri aktarın.
- (ör. sinavpuan, uyku_suresi, kilo)

4. Grafik ve Test Ayarlarını Yapın

Açılan pencerede sağ alttaki Plots... butonuna tıklayın.
Descriptive bölümünde:
- Histogram kutucuğunu işaretleyin.
- Normality plots with tests kutucuğunu işaretleyin (bu, Shapiro-Wilk ve Kolmogorov-Smirnov testlerini otomatik olarak ekler).
Continue ile pencereye geri dönün.

5. Analizi Başlat

OK butonuna tıklayın.

Normallik Analizinin Yorumlanması

Adım I ve II - Ortalama, Medyan, Mod & Çarpıklık (Skewness) ve Basıklık (Kurtosis) Katsayıları:

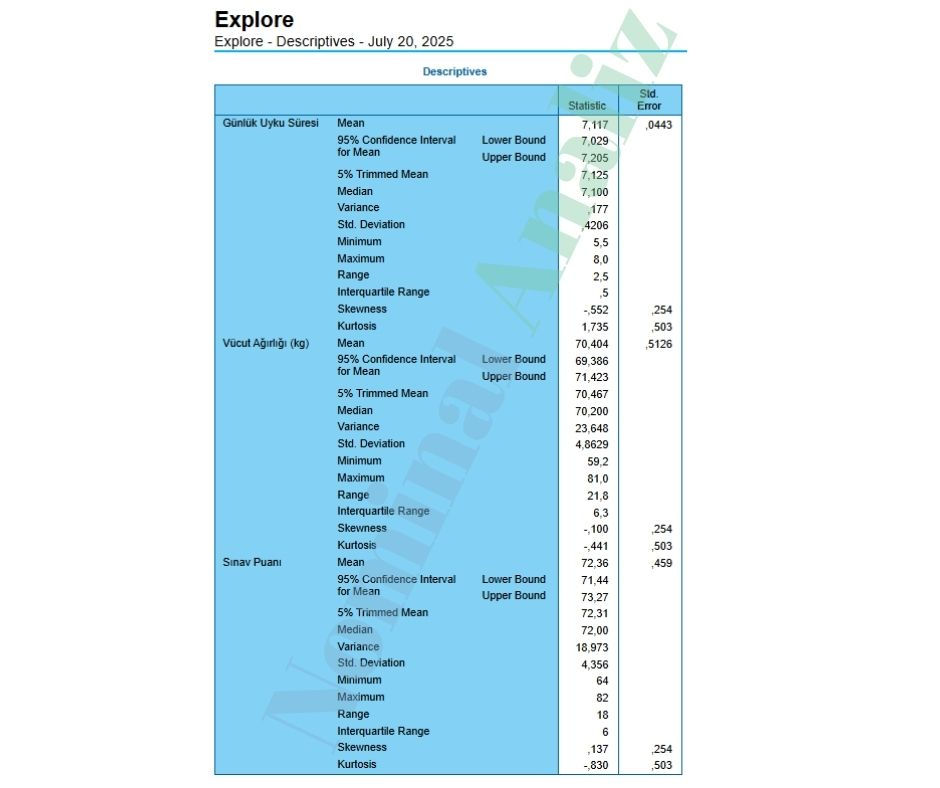
1. Temel İstatistikler ve Normallik Kriterleri

Bir veri setinin normal dağılıma uygunluğunu değerlendirmek için önce şu temel istatistiklere bakılır:

Ortalama (Mean) ve Medyan değerleri birbirine yakın mı?
Çarpıklık (Skewness) ve Basıklık (Kurtosis) katsayıları -1 ile +1 aralığında mı?
Değerlerin minimum ve maksimumları, standart sapması ve varyansı mantıklı ve veri setinin geneline uygun mu?

a) Günlük Uyku Süresi

Ortalama: 7,12 saat
Medyan: 7,10 saat
Minimum / Maksimum: 5,5 - 8,0 saat
Çarpıklık (Skewness): -0,552
Basıklık (Kurtosis): 1,735

Yorum: Ortalama ve medyan birbirine oldukça yakın. Çarpıklık değeri -1 ile +1 aralığında, bu da dağılımın simetriye yakın olduğunu gösterir. Ancak basıklık değeri 1,735 ile biraz yüksek; bu da dağılımın merkezi etrafında daha “sivri” olduğunu gösterir. Yine de temel olarak normal dağılıma yakın olduğu söylenebilir, fakat uç değer yoğunluğu biraz daha fazladır.

b) Vücut Ağırlığı (kg)

Ortalama: 70,40 kg
Medyan: 70,20 kg
Minimum / Maksimum: 59,2 - 81,0 kg
Çarpıklık (Skewness): -0,100
Basıklık (Kurtosis): -0,441

Yorum: Ortalama ile medyan neredeyse eşit; çarpıklık değeri -0,100 ile dağılım simetrik. Basıklık değeri -0,441, yani dağılım hafifçe basık, yani uç değerler merkezi çok sıkıştırmıyor. Bu açıdan vücut ağırlığı verisi neredeyse ideal bir normal dağılım gösteriyor.

c) Sınav Puanı

Ortalama: 72,36
Medyan: 72,00
Minimum / Maksimum: 64 - 82
Çarpıklık (Skewness): 0,137
Basıklık (Kurtosis): -0,830

Yorum: Ortalama ile medyan birbirine çok yakın; çarpıklık değeri 0,137 ve basıklık -0,830 ile normal dağılıma oldukça uygun. Dağılımda belirgin bir asimetri ya da uç değer baskınlığı yoktur.

Adım III - Histogram ve Q-Q Plot:

Günlük Uyku Süresi Değişkeni: Grafiklerin Yorumlanması:

1. Histogram İncelemesi

Histogram grafiği bize uyku süresi dağılımının genel şeklini gösteriyor.
Grafik, çan eğrisine yakın bir dağılım sunmakta; en fazla kişi 7 saat civarı uyuyor.
Sağ ve sol uçlarda (özellikle 6 saatin altında ve 8 saatin üzerinde) daha az gözlem bulunmakta.
Ortalama: 7,12 saat | Standart Sapma: 0,42 saat | N=90

Yorum: Histogram, verinin merkezi etrafında toplandığını ve uçlarda çok fazla değer olmadığını gösteriyor. Çan eğrisi şekline yakın olması normalliğin ilk görsel ipucu.

2. Stem-and-Leaf (Sap ve Yaprak) Grafiği (Veriler Çıktı Dosyasında Mevcuttur)

En fazla gözlem 7,0-7,4 arası (45 kişi) ve 6,5-6,9 arası (25 kişi).
6 saatin altında (2 kişi) ve 8 saatte (2 kişi) çok az veri var.
Dağılım büyük ölçüde merkezi bir kümelenme gösteriyor.

Yorum: Sap ve yaprak grafiği, veri noktalarının ağırlıklı olarak ortalamaya yakın değerlere sahip olduğunu gösteriyor; bu da normalliği destekliyor.

3. Q-Q Plot (Normal Q-Q Grafiği)

Noktaların çoğu diyagonal (45 derece) çizgiye yakın yerleşmiş.
Sadece birkaç uç değer çizgiden hafif sapma gösteriyor.

Yorum: Noktaların çizgi üzerinde ya da çok yakınında olması, verinin normal dağıldığının güçlü bir göstergesidir. Uçlardaki sapmalar çoğu zaman kabul edilebilir.

4. Detrended Q-Q Plot

Çoğu nokta yatay eksen üzerinde ve çevresinde toplanmış.
Az sayıda sapma gözlenmekte.

Yorum: Sapmalar genellikle uçlarda olur. Çoğunluk çizgiye yakınsa, bu da normal dağılıma uygunluğa işarettir.

5. Boxplot (Kutu Grafiği)

Kutu orta noktada (medyan 7 saat civarı).
Alt ve üst uçlarda birkaç "outlier" (aykırı değer) var, fakat bunlar verinin genel dağılımını bozacak düzeyde değil.

Yorum: Medyan ile ortalama birbirine yakın. Kutu simetrik; bu da normallik için olumlu.

Vücut Ağırlığı (kg) Değişkeni: Grafiklerin Yorumlanması:

1. Histogram Yorumu

Histogram grafiği, vücut ağırlığı değerlerinin çoğunlukla 65-75 kg arasında toplandığını, dağılımın iki uca doğru kademeli olarak azaldığını göstermektedir. En yüksek frekans, ortalama civarındaki değerlerde toplanmıştır. Çubukların çoğunluğu merkezde yoğunlaşıyor ve uçlarda birkaç düşük frekanslı çubuk var. Bu görünüm, dağılımın yaklaşık simetrik ve çan eğrisi (normal dağılım) benzeri olduğunu gösteriyor.

2. Stem-and-Leaf Plot Yorumu (Veriler Çıktı Dosyasında Mevcuttur)

Stem-and-leaf plot’ta da değerler, 60’lı ve 70’li kilogramlar arasında yoğunlaşmakta. Özellikle 65-75 kg arası yoğunluk dikkat çekici. Uçlarda (59 ve 81 kg) yalnızca birer değer var; bunlar veri setinin uç değerleri. Merkezdeki yığılma, dağılımın merkezî bir eğilim gösterdiğine işaret eder ve normal dağılım varsayımını destekler.

3. Q-Q Plot Yorumu

Normal Q-Q plot grafiği, gözlenen vücut ağırlığı değerlerinin büyük kısmının diyagonal çizgi üzerinde ya da çizgiye yakın noktalandığını gösteriyor. Diyagonalden fazla sapma yok, yalnızca uçlarda hafif oynamalar var. Bu, vücut ağırlığı verisinin normal dağılım varsayımına oldukça uygun olduğunu gösterir.

4. Detrended Q-Q Plot Yorumu

Detrended Q-Q plot’ta gözlemlenen noktalar çoğunlukla yatay eksen etrafında toplanmış durumda. Merkezdeki noktalar çizgiye yakın ve sapmalar minimal. Özellikle uçlarda (minimum ve maksimum değerler) hafif sapmalar gözleniyor. Ancak bu sapmalar, tipik büyük örneklemlerde her zaman görülebilir ve ciddi bir normal dağılım ihlali olduğunu göstermez.

5. Boxplot Yorumu

Boxplot’ta medyan (orta çizgi), kutunun ortasında yer almakta ve kutu simetrik görünüyor. Alt ve üst sınır değerlerinde ciddi bir uç değer (outlier) yok; sadece birkaç uç noktada veri var. Bu da veri setinin dağılımının düzgün ve dengeli olduğunu gösterir.

Genel Değerlendirme & Sonuç

Vücut Ağırlığı (kg) değişkenine ait tüm grafikler (histogram, Q-Q plot, boxplot) incelendiğinde, veri setinin normal dağılım varsayımını karşıladığını rahatlıkla söyleyebiliriz.
Hafif uç sapmalar olsa da, merkezdeki yığılma ve çan eğrisi görüntüsü, istatistiksel testlerde parametrik yöntemlerin kullanılabileceğine işaret eder.
Büyük örneklemlerde uç değerler çok önemli bir problem teşkil etmez; önemli olan merkezdeki simetri ve dağılımın şeklidir.

Sınav Puanı Değişkeni: Grafiklerin Yorumlanması:

1. Histogram Yorumu

Histogram grafiği, sınav puanlarının dağılımını görsel olarak ortaya koyar. Veriler yaklaşık olarak ortalama (Mean = 72,36) çevresinde yoğunlaşmakta, sağ ve sol kanatlarda ise daha az sayıda gözlem yer almakta. Grafikteki çubukların çoğu orta değerlere yakın olup, uçlarda azalan sıklıkla veriler gözlenmiştir. Bu yapı, çan eğrisi olarak bilinen normal dağılım formuna oldukça yakındır. Yani veri setinde ciddi bir çarpıklık (skewness) ya da uç değer (kuyruk uzunluğu) görünmemektedir.

2. Stem-and-Leaf Plot Yorumu (Veriler Çıktı Dosyasında Mevcuttur)

Sap-çizelgesi, sınav puanlarının ham dağılımını detaylı biçimde göstermektedir. En yüksek sıklık, 70’li ve 60’lı puanlar arasındadır. Puanlar geniş bir aralıkta (64 ile 82 arası) dağılmıştır. Yine burada da orta kısımlarda birikim, uçlarda azalma vardır. Veri setinde belirgin bir uç değer (extreme value) yoktur, bu da normallik açısından olumlu bir göstergedir.

3. Q-Q Plot (Normal Kuantille-Kuantil Grafiği) Yorumu

Q-Q plot, gözlenen puanların beklenen normal değerlerle kıyaslandığı bir grafiktir. Noktalar, referans çizgisi üzerinde ve çevresinde oldukça düzgün bir şekilde dizilmiş durumda. Özellikle merkezi değerlerde (70-75 puan arası) gözlenen ve beklenen değerler neredeyse tamamen örtüşüyor. Çok uçlardaki birkaç nokta referans çizgiden hafifçe sapmış olsa da bu doğal kabul edilir. Buradaki genel görünüm, sınav puanlarının normal dağılıma uygun olduğunu göstermektedir.

4. Detrended Q-Q Plot Yorumu

Bu grafik, normal Q-Q plot’taki sapmaların daha rahat görülmesini sağlar. Noktaların çoğu yatay eksen (sıfır çizgisi) çevresinde küçük dalgalanmalarla seyretmekte, büyük sapmalar veya sistematik bir bozulma yok. Bu da normal dağılımdan anlamlı bir sapmanın olmadığını destekler.

5. Boxplot Yorumu

Boxplot, sınav puanlarının genel dağılımını ve olası uç değerleri (outlier) görmemizi sağlar. Kutunun merkezi çizgisi (medyan) ile kutunun sınırları (alt ve üst çeyrekler) birbirine yakın. Veri dağılımı dengeli ve simetrik görünüyor. Ayrıca belirgin bir aykırı değer yok.

Sonuç & Genel Yorum

Sınav Puanı değişkeni, SPSS çıktılarında yer alan tüm grafikler (histogram, Q-Q plot, detrended Q-Q plot ve boxplot) açısından incelendiğinde normal dağılıma yakın bir görünüm sergilemektedir.
Veriler, ortalama ve medyan çevresinde toplanmakta ve ciddi bir uç değer (outlier) barındırmamaktadır.
Q-Q plot ve detrended Q-Q plot analizleri, dağılımın normal olduğunu güçlü biçimde desteklemektedir.
Boxplot’ta aykırı değer bulunmaması da normalliği pekiştirir.

Bu sonuçlara göre, Sınav Puanı değişkeni için parametrik testler (örneğin Tek Örneklem t Testi) uygulanabilir.

Adım IV - Normallik Testlerinin İncelenmesi & Yorumlanması:

Normallik Testleri Sonuçlarının Yorumlanması

1. Kriterler ve Yöntem

Kolmogorov-Smirnov testi: Örneklem büyüklüğü 30 ve üzerinde olduğunda tercih edilir (bizim örneklemimiz N=90, yani bu test uygun).
Shapiro-Wilk testi: Daha küçük örneklemler için önerilir, ancak SPSS her iki testi de sunar.
Temel yorumlama kuralı:
- p > 0,05 ise dağılım normaldir (normallik varsayımı sağlanır).
- p < 0,05 ise dağılım normal değildir (normallik varsayımı sağlanmaz).