Lojistik Regresyon Z-Testi Güç Analizi: İki Farklı Senaryonun Karşılaştırmalı İncelemesi

Lojistik regresyon, ikili (0–1) sonuç değişkenleri için en sık kullanılan modellerden biridir. Bir olayın gerçekleşip gerçekleşmediğini tahmin ederken, bağımsız değişkenlerin bu olasılıklar üzerindeki etkisini modellemeyi sağlar. Bu yazıda G*Power kullanarak iki farklı senaryo üzerinden Lojistik regresyon gücünü hesaplayacağız:

• Senaryo 1: Odds ratio (OR) üzerinden güç analizi (a priori).

• Senaryo 2: İki olasılık (p1 ve p2) üzerinden güç analizi (a priori).

Her iki senaryoda da Hsieh et al. (1998) ve Demidenko (2007) prosedürlerine dayalı örnekleri kullanıyoruz.

1.Teorik Çerçeve

1.1 Lojistik Regresyon ve Güç Analizi

• Lojistik regresyonda bağımlı değişken Y (0 veya 1) bir olayın oluşup oluşmadığını gösterir.

• Odds Ratio (OR), bağımsız değişken X’in Y üzerindeki etkisini ölçer. OR>1 artış, OR<1 azalış anlamına gelir.

• G*Power bu modeller için Wald testi temelli güç analizi yapar.

1.2 İki Analiz Yaklaşımı

1. Odds Ratio Mode: Tek bir OR değeri üzerinden etki büyüklüğünü belirtirsiniz.

2. Two Probabilities Mode: Hem H0 hem H1 altında olay olasılıklarını girersiniz.

Her iki yöntem de sonuçta testin gücünü veya gerekli örneklem büyüklüğünü hesaplar.

2. Senaryo 1: Odds Ratio Üzerinden A Priori Analiz

Amaç: Olasılık p1=0.5 altında, X’in Y üzerindeki etkisini OR=1.5 olarak alıp 0.95 güçle kaç örneğe ihtiyaç olduğunu bulmak.

Girdi Parametreleri:

• Test: Logistic Regression

• Type of power analysis: A priori

• Effect size input mode: Odds ratio

• Procedure: Hsieh et al. (1998)

• Tail(s): Two

• Odds ratio: 1.5

• Pr(Y=1) H0: 0.5

• α err prob: 0.05

• Power (1-β err prob): 0.95

• R² other X: 0

• X distribution: Normal

• X param μ: 0

• X param σ: 1

Çıktı (Hsieh et al. 1998):

• Kritik z: 1.959964

• Gerekli minimum örneklem: 337

• Actual power: 0.950077

Alternatif Prosedürler:

• Demidenko (2007) variance correction: N=337

• Demidenko (2007) no correction: N=355

• Enumeration (Lyles et al. 2007): N=358

Yorum: OR=1.5 gibi orta büyüklükte bir etki için 0.95 güç hedefleniyorsa yaklaşık 317–355 örnek gerekir. Variance correction’lı Demidenko yöntemi en iyi tahmini verir.

3. Senaryo 2: İki Olasılık Üzerinden A Priori Analiz

Amaç: X=1 altında p2=0.1 ve X=0 altında p1=0.05 olasılıkları için 0.95 güçle kaç örneğe ihtiyaç olduğunu bulmak.

Odds ratio Hesaplaması:

Girdi Parametreleri:

• Test: Logistic Regression

• Type of power analysis: A priori

• Effect size input mode: Two probabilities

• Tail(s): Two

• Pr(Y=1|X=1) H1: 0.1

• Pr(Y=1|X=1) H0: 0.05

• α err prob: 0.05

• Power (1-β err prob): 0.95

• R² other X: 0

• X distribution: Binomial

• X param π: 0.5 (dengeli tasarım)

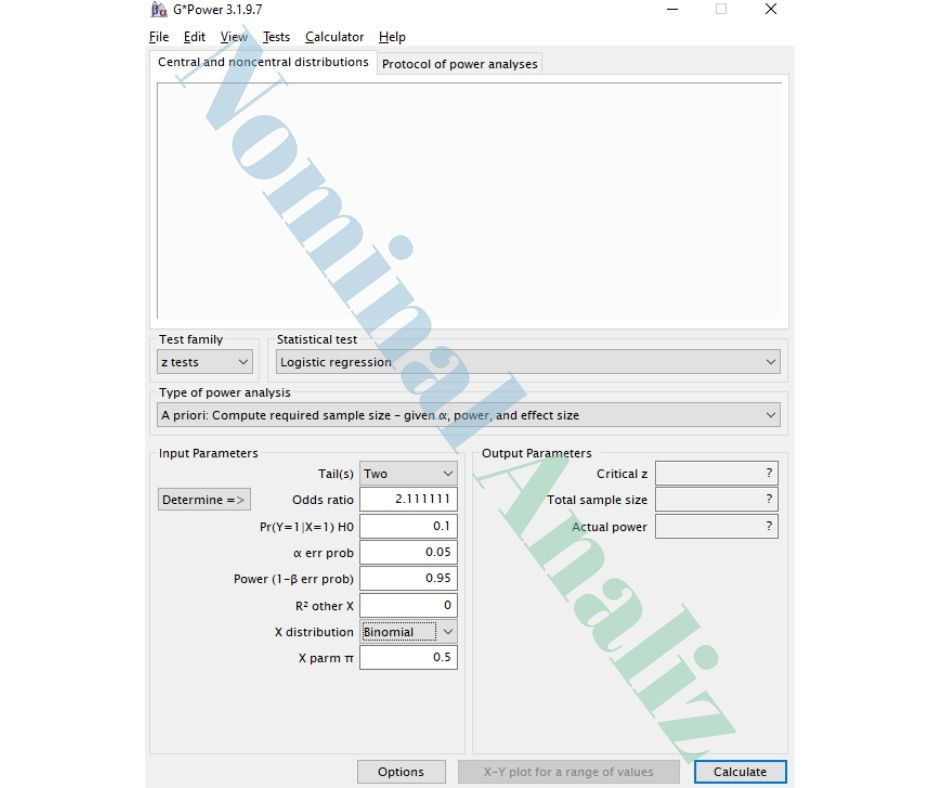
Çıktı (Hsieh et al. 1998):

• Kritik z: 1.9599640

• Gerekli toplam örneklem: 793

• Actual power: 0.9500620

Alternatif Prosedürler:

• Demidenko (2007) variance correction: N=1498

• Daha düşük veya yüksek π değerleri kullanıldığında (örneğin π=0.2 veya π=0.8), gerekli örneklem sayısı 2158–2368 aralığına çıkar.

Yorum: p1=0.05, p2=0.1 gibi küçük olasılıklar bile ciddi örneklem artışına yol açar. Denge faktörü (π) örneklem büyüklüğü üzerinde büyük etkiye sahiptir.

4. Karşılaştırmalı Tablo

Parametre / Çıktı	Senaryo 1 (OR=1.5)	Senaryo 2 (p1=0.05 p2=0.1)
Analiz türü	A priori	A priori
Etki büyüklüğü	Odds ratio 1.5	p1=0.05, p2=0.1
X dağılımı	Normal	Binomial π=0.5
Hedef güç (1-β)	0.95	0.95
α	0.05	0.05
Gerekli örneklem (Hsieh)	337	793
Gerekli örneklem (Demidenko + corr)	337	1498

• Logistic regresyonda güç analizi yapılırken etki büyüklüğü tanımlama biçimi (OR veya p1/p2) sonuçları doğrudan etkiler.

• Demidenko (2007) yöntemi, özellikle büyük örneklemlerde ve variance correction açıkken en doğru tahminleri verir.

• Dengeli tasarım (π=0.5) daha az örneklem gerektirir; dengesiz tasarımlar (π=0.2 veya 0.8) örneklem ihtiyacını dramatik şekilde artırır.

• Önceden yapılan a priori analizler, çalışmanın güçlü ve güvenilir sonuçlar vermesini sağlar.