Histogram Nedir? Teorik Açıklama ve Örnek Grafik Yorumlama

Histogramın Tanımı

Histogram, sürekli ya da aralıklı nicel (sayısal) verilerin frekans dağılımını görselleştiren bir grafik türüdür. En önemli özelliği, verileri belirli aralıklara (binlere) böler ve her aralıktaki gözlem sayısını (frekansı) çubuklarla (dikdörtgenlerle) gösterir.

Histogramlar, verinin yayılımını, merkezi eğilimini ve varsa uç (aykırı) değerlerini hızla fark etmemize olanak sağlar.

Histogramın Temel Özellikleri

• X ekseni: Verinin değer aralıklarını (bin aralıkları) gösterir.

• Y ekseni: Her bir aralıkta (bin) bulunan gözlem/frekans sayısını gösterir.

• Çubuklar bitişiktir: Çünkü aralıklı/sürekli verilerde değerler birbirini takip eder (örneğin, yaş, gelir, sıcaklık).

• Bin genişliği: Tüm binler (aralıklar) genellikle eşit genişliktedir; bu sayede dağılımın genel görünümü bozulmaz.

Kendi Örneğimle Histogram: Öğrenci Sınav Sonuçları

Veri: Bir sınıfta 20 öğrencinin matematik sınavından aldığı puanlar şöyle olsun:

58, 60, 61, 63, 65, 66, 68, 68, 69, 70, 70, 72, 75, 76, 77, 80, 82, 85, 90, 95

1. Bin Aralıklarını Belirleyelim

Puanlar 58 ile 95 arasında değişiyor. Bin genişliğini 10 seçersek aralıklarımız:

• 50–60

• 60–70

• 70–80

• 80–90

• 90–100

2. Her Aralıktaki Öğrenci Sayısı

• 50–60: 1 öğrenci (58)

• 60–70: 8 öğrenci (60, 61, 63, 65, 66, 68, 68, 69)

• 70–80: 5 öğrenci (70, 70, 72, 75, 76, 77)

• 80–90: 3 öğrenci (80, 82, 85)

• 90–100: 1 öğrenci (90, 95)

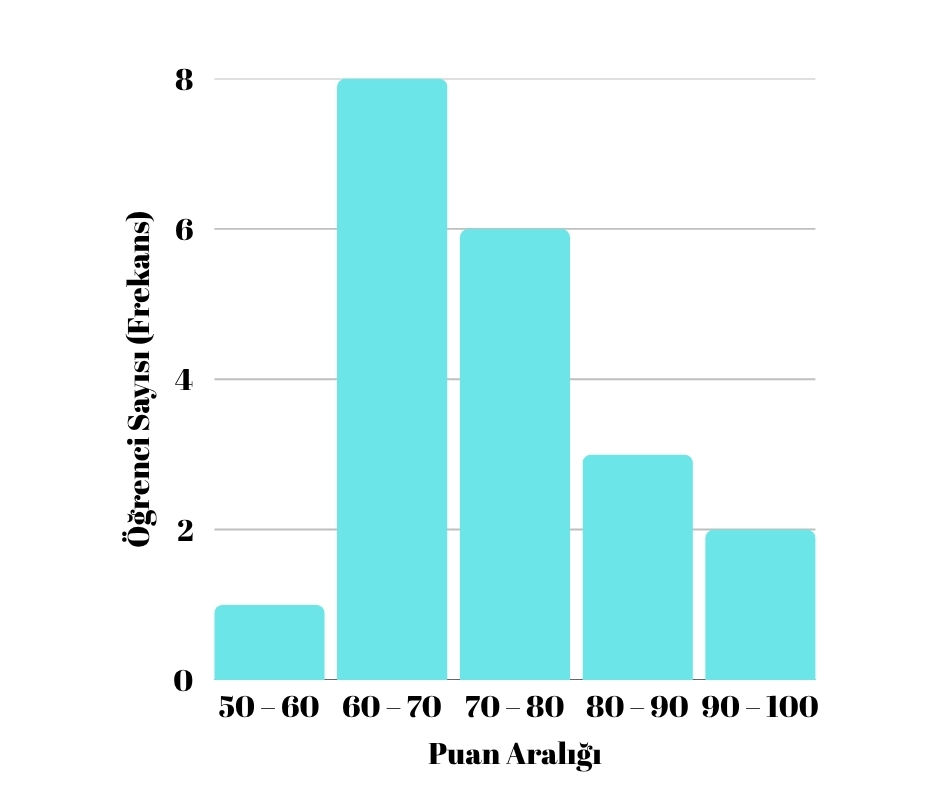
3. Histogram Grafiğinin Yorumu

Grafikte;

• En yüksek çubuk 60–70 aralığında (8 öğrenciyle).

• 70–80 aralığında orta yükseklikte bir çubuk.

• 80–90 ve 50–60 aralıklarında düşük çubuklar.

• 90–100 aralığında ise yalnızca 1 öğrenci var.

4. Analiz ve Açıklama

• Dağılımın Merkezi: En yoğun aralık 60–70 (sınıf puanları burada toplanmış).

• Sola çarpık dağılım var; çünkü yüksek puanlar daha az, düşük puanlar daha çok.

• Aykırı değer yok: Çok uçta tek bir öğrenci yok, tüm puanlar makul aralıklarda.

• Kullanım Alanı: Bu histogram, öğretmene hangi puan aralığında en fazla öğrencinin olduğunu, genel başarı düzeyini ve istatistiksel dağılımı kolayca gösterir.

Histogram Niçin ve Nasıl Kullanılır?

• Veri dağılımı hakkında hızlı fikir verir.

• Normal dağılıma yakınlık/uzaklık anlaşılır.

• Aykırı ve uç değerler hızla fark edilir.

• Verilerin hangi aralıklarda yoğunlaştığı görülür.

• İstatistiksel analizler öncesi veri yapısı hakkında öngörü sağlar.