G*Power ile t Testi: Doğrusal Regresyon (Eğim Büyüklüğü, Tek Grup)
- Nominal Analiz
- 23 Ağu 2025
- 2 dakikada okunur
Bu yazıda G*Power kullanılarak doğrusal regresyon analizi kapsamında yapılan özel bir t testi incelenecektir: Linear Regression – size of slope, one group.
Bu prosedür, bir bağımlı değişken (Y) ile bağımsız değişken (X) arasındaki doğrusal ilişkinin eğiminin (slope b) belirli bir değerden farklı olup olmadığını test eder.
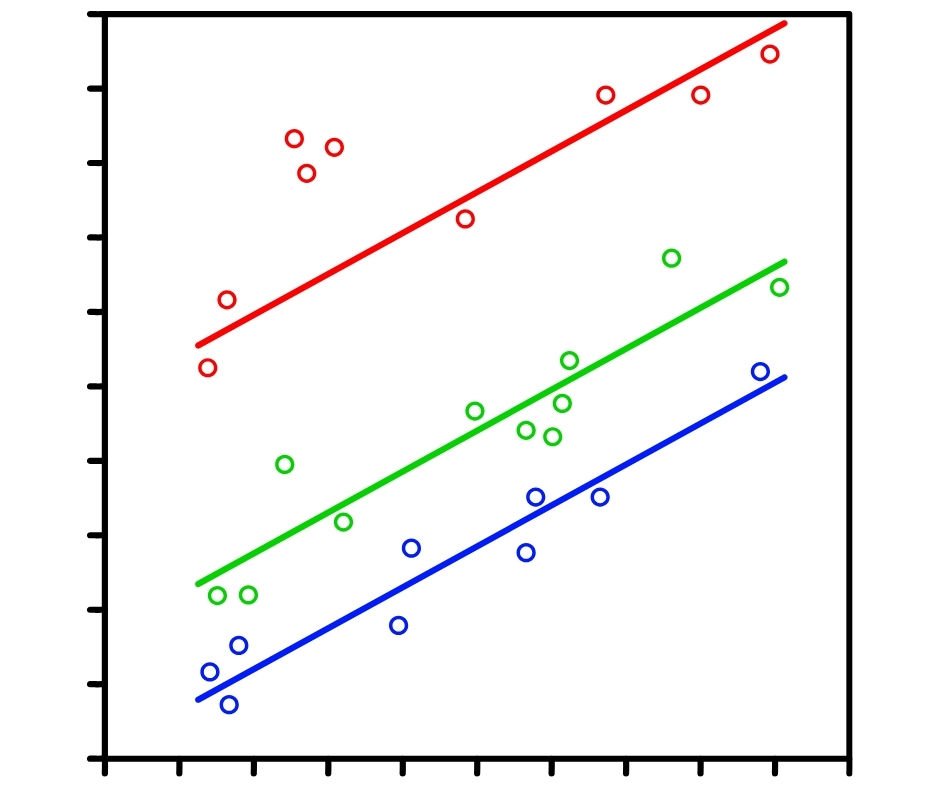
🔎 Doğrusal Regresyon ve Hipotez Yapısı
Doğrusal regresyon modeli:
Y = a + bX + ε
X: Bağımsız değişken (sabit değerler)
Y: Bağımlı değişken (rastgele değişken)
ε: Hata terimi (ortalama = 0, σ sabit varyans)
Hipotezler:
H0: b – b0 = 0 (eğim sabit b0 değerine eşit)
H1: b – b0 ≠ 0 (eğim b0’dan farklı)
Örnek: Bir eğitim programında günlük egzersiz süresinin vücut kitle indeksi (BMI) üzerindeki etkisi araştırılsın. Burada b0 = 0 iken, H1 altında b negatif (egzersiz süresi arttıkça BMI düşüyor).
📐 Etki Büyüklüğü (Effect Size Index)
Etki büyüklüğü, eğimin H1 altındaki değeri (Slope H1) üzerinden hesaplanır. Bunun için:
Slope H0: H0 altında varsayılan eğim değeri (genellikle b0 = 0).
Std dev σx: X değişkeninin standart sapması.
Std dev σy: Y değişkeninin standart sapması.
σy ayrıca şu ilişkilerle hesaplanabilir:
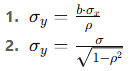
Burada:
σ → artıkların (residuals) standart sapması,
ρ → X ve Y arasındaki korelasyon katsayısıdır.
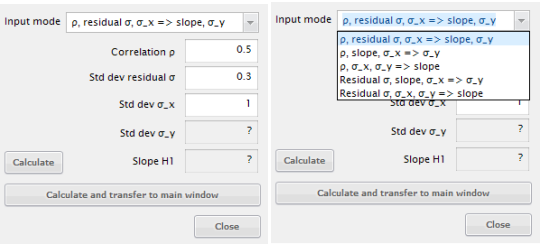
G*Power Etki Büyüklüğü Paneli (Şekil 15)
Farklı giriş modlarıyla (ρ, σ, σx, σy) eğim b hesaplanabilir.
“Calculate and transfer” butonuyla değerler ana pencereye aktarılır.
⚙️ Örnek Uygulama (Dupont ve Plummer, 1998)
Araştırma Sorusu:Egzersiz süresi ile BMI arasında anlamlı bir ilişki var mı?
Veriler:
σx (egzersiz süresi sd) = 7.5 dk
σy (BMI sd) = 4
Örneklem büyüklüğü N = 100
α = 0.05
H1 eğimi b = -0.0667 (30 dk egzersiz → BMI’de 2 puan düşüş)
G*Power Ayarları:
Tail(s): İki yönlü
Effect size Slope H1: -0.0667
Slope H0: 0
Std dev σx: 7.5
Std dev σy: 4
Total N: 100
Sonuç:
Noncentrality parametresi δ = 1.26
Kritik t = ±1.98
Güç (1-β) = 0.239 ≈ %24
👉 Bu, çalışmanın düşük güce sahip olduğunu (sonucun güvenilir olmayabileceğini) gösterir.
🔗 Çoklu Regresyon ile İlişki
Bu prosedür aslında çoklu regresyon testinin özel bir durumudur (tek yordayıcı).
Bağlantı şu formülle gösterilir:
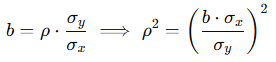
Örneğin:
(−0.0667⋅7.5 / 4) ^ 2 = 0.0156 ⇒ R^2= 0.0156.
Bu değer G*Power’daki “Multiple Regression: Omnibus” seçeneğinde kullanıldığında aynı güç (0.24) elde edilir.
Doğrusal regresyon eğim testi, bağımsız değişken ile bağımlı değişken arasındaki ilişkinin yönünü ve gücünü test etmede kritik öneme sahiptir.
Etki büyüklüğü, eğim b’nin büyüklüğüne, σx ve σy’ye bağlıdır.
G*Power, bu test için gerekli örneklem büyüklüğünü hesaplamada ve mevcut örneklemle güç analizi yapmada etkin bir araçtır.
Örnekte görüldüğü gibi düşük etki büyüklükleri, yeterli örneklem büyüklüğü olmadan düşük güç üretir.








Yorumlar