G*Power ile Kesin Test: Çoklu Regresyon – Rassal Model

Çoklu regresyon analizleri, bir bağımlı değişken Y ile birden fazla bağımsız değişken X = (X₁, …, Xₘ) arasındaki ilişkinin incelenmesini sağlar. Klasik yaklaşımda (fixed model) bağımsız değişkenler sabit kabul edilirken, random model yaklaşımında hem bağımlı hem de bağımsız değişkenler rassal değişkenlerdir.

Bu nedenle güç analizi ve örneklem büyüklüğü hesaplamaları, fixed modele göre farklılık gösterir.

Random model, Gatsonis & Sampson (1989) ve Sampson (1974) tarafından geliştirilmiş olup, araştırmalarda bağımsız değişkenlerin rastlantısal varyasyonunun da hesaba katılmasına imkân tanır.

Teorik Çerçeve

Y ve X vektörlerinin ortak dağılımı çok değişkenli normaldir:

Ortak kovaryans matrisi:

Burada, ΣX pozitif tanımlı bir kovaryans matrisi,ΣYX​ ise Y ile bağımsız değişkenler arasındaki kovaryans vektörüdür.

Popülasyon Çoklu Korelasyon Katsayısı

Regresyon katsayı vektörü ise:

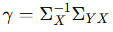
Hipotezler

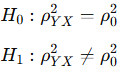
Özel bir durumda, bağımlı değişken ile tüm bağımsız değişkenler arasındaki ilişkinin sıfır olduğu varsayılır. Bu durumda kullanılan test istatistiği:

Etki Büyüklüğü

Etki büyüklüğü, popülasyon çoklu korelasyon katsayısının karesi üzerinden tanımlanır:

Cohen (1988) standart değerler:

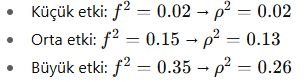
Etki Büyüklüğünün Belirlenmesi

1. Güven Aralığından (Confidence Interval):

2. Yordayıcı Korelasyonlarından (Predictor Correlations):

Burada:

• u = bağımlı değişken ile her bir yordayıcı arasındaki korelasyon vektörü

• B = yordayıcılar arasındaki korelasyon matrisi

Matrisin pozitif tanımlı olması gerekir.

Örnek 1 – Güç Hesaplama

G*Power çıktısı:

• Kritik R2R^2R2 = 0.115

• Güç = 0.663

Bu değer, aynı senaryonun fixed modeldeki gücünden (0.674) daha düşüktür. Genel olarak random modelin gücü fixed modelden daha düşük çıkar.

Örnek 2 – Belirli Hipotez Testi

Bu durumda örneklem yetersiz kalmaktadır.

Örnek 3 – Minimum Örneklem Büyüklüğü

Örnek 4 – Güven Aralığından Etki Büyüklüğü

Örnek 5 – Korelasyon Matrisi ile Etki Büyüklüğü

• 4 yordayıcı: u = (0.3,0.1,−0.2,0.2)

• Korelasyon matrisi:

Yaklaşımlar ve Dağılımlar

• G*Power, exact sampling distribution (MRC dağılımı) kullanır.

• Alternatif olarak Lee (1971) tarafından önerilen üç momentli F yaklaşımı seçilebilir. Bu yöntem daha hızlıdır ancak yalnızca doğrulama amacıyla kullanılması tavsiye edilir.

Yöntemin Güvenirliği ve Karşılaştırmalar

G*Power’ın kullandığı algoritmalar Benton & Krishnamoorthy (2003) yaklaşımına dayanır.Bu yöntem, Ding (1996) gibi eski algoritmalardaki hesaplama hatalarını ve büyük örneklemlerdeki taşma (overflow) problemlerini ortadan kaldırır.

Güç ve örneklem büyüklüğü sonuçları, literatürdeki tablolar (Gatsonis & Sampson, 1989; Shieh & Kung, 2007) ve R² programı (Steiger & Fouladi, 1992) ile karşılaştırılarak doğrulanmıştır.