G*Power ile Fisher’s Exact Test: İki Bağımsız Grup Oran Karşılaştırmalarında Güç Analizi

İstatistiksel araştırmalarda iki bağımsız grubun başarı oranlarını karşılaştırmak sıkça karşılaşılan bir durumdur. Özellikle örneklem büyüklüğü küçük olduğunda, klasik ki-kare testlerinin yanıltıcı sonuçlar verebilmesi nedeniyle Fisher’s Exact Test daha güvenilir bir yaklaşım sunar.

Bu test, hipotez testi ve güç analizi açısından G*Power yazılımı ile birlikte kullanıldığında araştırmacıya hem teorik hem de pratik düzeyde güçlü bir analiz zemini sağlar.

Fisher’s Exact Test’in Kuramsal Çerçevesi

İki bağımsız grubun başarı ve başarısızlık oranlarını karşılaştırmak için veriler 2×2 kontenjans tablosu şeklinde özetlenir:

	Grup 1	Grup 2	Toplam
Başarı	x₁	x₂	m
Başarısızlık	n₁−x₁	n₂−x₂	N−m
Toplam	n₁	n₂	N

Burada, n₁ ve n₂ örneklem büyüklüklerini, x₁ ve x₂ gözlenen başarı sayılarını ifade eder.

Hipotezler:

• H0 : π1 = π2

• H1 : π1 ≠ π2

Burada π1 ve π2​, her iki grubun başarı olasılıklarını göstermektedir.

Etki Büyüklüğü

Etki büyüklüğü doğrudan iki grubun başarı olasılıkları arasındaki fark ile tanımlanır:

Δ = ∣π1−π2∣

Örneğin, bir çalışmada π1 = 0.40 ve π2 = 0.70 ise, etki büyüklüğü Δ = 0.30 olur.

Test İstatistiği ve Olasılık Dağılımı

Fisher’s Exact Test, olasılıkların hiper-geometrik dağılım üzerinden hesaplanmasına dayanır.

H0 altında gözlenen tabloyun olasılığı:

Test istatistiği T, üç farklı şekilde tanımlanabilir:

• Fisher’s exact test:

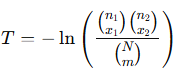
• Pearson’un exact testi:

• Likelihood ratio exact testi:

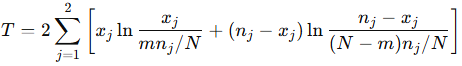
Bu istatistikler, p-değerinin hesaplanma şeklini etkiler fakat asimptotik olarak benzer sonuçlara götürür.

Güç (Power) Hesabı

Güç, testin gerçekte var olan bir farkı yakalama olasılığıdır.

Genel ifade:

Burada:

• P(m), H1 altında toplam başarı sayısının dağılımıdır.

• tα​, kritik değer olup, Pr(T ≥ tα∣H0) ≤α koşulunu sağlar.

H1 altında tablo olasılığı:

Dolayısıyla:

G*Power ile Uygulama

G*Power yazılımı, bu karmaşık hesaplamaları otomatikleştirerek araştırmacıya pratik bir çözüm sunar.

Örneğin bir senaryoda:

• Grup 1 (klasik yöntem): n₁ = 20, başarı oranı = 0.40

• Grup 2 (yeni yöntem): n₂ = 20, başarı oranı = 0.70

• α = 0.05 (iki yönlü test)

G*Power çıktısına göre güç değeri yaklaşık %62’dir. Bu oran, istatistiksel anlamlılık için düşük kabul edilir. Daha güvenilir bir test için örneklem büyüklüklerinin artırılması gerekir.

Eğer örneklem büyüklükleri n₁ = n₂ = 40 olacak şekilde iki katına çıkarılırsa, aynı etki büyüklüğü için güç değeri yaklaşık %80’e yükselir.

Uygulamalı Örnek Tablo

	Başarı	Başarısızlık	Toplam
Grup 1	8	12	20
Grup 2	14	6	20
Toplam	22	18	40

Fisher’s Exact Test ile yapılan analiz:

• p ≈ 0.047

• α = 0.05 → anlamlı fark vardır.

• Güç (power) ≈ %62

G*Power simülasyonu ile bu tablo daha geniş örneklemlere uyarlanabilir ve araştırmacı, çalışmaya başlamadan önce gerekli örneklem büyüklüğünü belirleyebilir.