G*Power ile F Testi: Çoklu Regresyon – Omnibus (R²’nin Sıfırdan Sapması)

Çoklu regresyon (multiple regression), bir bağımlı değişkenin (Y) birden fazla bağımsız değişken (X₁, X₂, …, Xm) ile olan ilişkisini modelleyen güçlü bir istatistiksel yöntemdir.

G*Power yazılımında kullanılan F Testi: Multiple Regression – Omnibus, bağımsız değişkenlerin birlikte bağımlı değişken üzerindeki açıklayıcılığını (R²) test eder.

🔎 Omnibus Testinin Mantığı

Bu prosedür, bağımlı değişken Y’nin varyansının bir grup yordayıcı tarafından açıklanan kısmının sıfır olup olmadığını test eder.

• H0: R² = 0 → Y değişkenini açıklayan varyans yok.

• H1: R² > 0 → Y değişkeninin varyansının en az bir kısmı bağımsız değişkenler tarafından açıklanıyor.

Matematiksel model:

Y = Xβ + ε

• X: Bağımsız değişkenler matrisi (sabit + m değişken).

• β: Regresyon katsayıları.

• ε: Hata terimleri (εi ∼ N(0, σ)).

📐 Etki Büyüklüğü (Effect Size f²)

Çoklu regresyon testlerinde kullanılan etki büyüklüğü:

ve tersine:

Cohen (1988) etki büyüklüğü ölçütleri:

• Küçük etki: f² = 0.02

• Orta etki: f² = 0.15

• Büyük etki: f² = 0.35

👉 Bu ölçütler, araştırmacının örneklem büyüklüğü planlamasında temel rol oynar.

⚙️ Etki Büyüklüğü Hesaplama Yöntemleri

G*Power yazılımı iki farklı yöntem sunar:

1. Korelasyon Katsayısından (R²)

Eğer R² doğrudan biliniyorsa, f² değeri formülle hesaplanır ve G*Power’a girilir.

2. Yordayıcılar Arası Korelasyonlardan

Eğer R² bilinmiyorsa, yordayıcı değişkenlerle (predictors) bağımlı değişken arasındaki korelasyonlar ve yordayıcıların kendi aralarındaki korelasyonlar kullanılarak hesaplanır:

• u: yordayıcılar ile Y arasındaki korelasyon vektörü,

• B: yordayıcılar arası korelasyon matrisi.

Sonuçta ρ² elde edilir → f² hesaplanır.

📊 Örnek 1: Temel Uygulama

• Y değişkenini 5 yordayıcı ile tahmin ediyoruz.

• Popülasyon R² = 0.10 (yordayıcılar Y’nin varyansının %10’unu açıklıyor).

• Örneklem büyüklüğü N = 95, α = 0.05.

G*Power Ayarları:

• Effect size f² = 0.111

• Predictors = 5

• N = 95

Sonuç:

• Noncentrality λ = 10.56

• Numerator df = 5

• Denominator df = 89

• Güç (1-β) = 0.674

👉 Güç yaklaşık %67’dir (orta düzey, daha büyük örneklem gerekebilir).

📊 Örnek 2: ANOVA ile İlişki

• Tek faktörlü ANOVA tasarımı (k = 4 grup, ortalamalar = 2, 3, 2, 5).

• Grup büyüklükleri: 5, 6, 6, 5.

• Ortak sd = 2.

ANOVA ile: f = 0.593 → güç ≈ 0.536.

MRC ile: f² = f² = 0.3517, predictors = k-1 = 3.Aynı örneklem ve α ile güç ≈ 0.536.

👉 Bu, ANOVA ve regresyon testlerinin matematiksel eşdeğerliğini gösterir.

📊 Örnek 3: Nokta-Biserial Korelasyon ile İlişki

Bir korelasyon r = 0.5 (r² = 0.25) olsun.

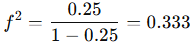
N = 12, α = 0.05 için güç ≈ 0.44.

👉 Bu analiz de çoklu regresyon prosedürüyle yapılabilir.

🔗 İlgili Testler

• Çoklu Regresyon: Özel (R² artışı)

• ANOVA: Tek yönlü, sabit etkiler

• İki bağımsız grubun ortalama farkı (t testi)

• Korelasyon: Nokta-biserial model

• Omnibus regresyon testi, çoklu regresyonun en temel hipotez testi olup, R²’nin sıfırdan anlamlı şekilde farklı olup olmadığını değerlendirir.

• Küçük etki büyüklüklerinde yeterli güç için büyük örneklemlere ihtiyaç vardır.

• Bu prosedür, ANOVA ve t testleri gibi yöntemlerle doğrudan ilişkilidir.

• G*Power, araştırmacılara örneklem büyüklüğü planlaması ve güç analizi için güçlü ve esnek bir araç sunar.