Çarpıklık (Skewness): Dağılımların Asimetrisini Anlama Rehberi

İstatistiksel analizlerde bir değişkenin dağılımını doğru yorumlamak, sonraki tüm adımların sağlıklı ilerlemesi için kritik öneme sahiptir. Çarpıklık (skewness) ise dağılımın simetrik olup olmadığını gösteren temel ölçülerden biridir. Bir dağılımın sağa ya da sola doğru uzayan bir kuyruğu varsa, bu durum hesaplanan ortalamadan çıkarımları etkileyebilir ve birçok istatistiksel testin varsayımlarını doğrudan ilgilendirir.

Aşağıda çarpıklığın ne olduğu, türleri, nasıl hesaplandığı ve çarpık verilerle nasıl başa çıkılabileceği detaylı biçimde ele alınmaktadır.

Çarpıklık Nedir?

Çarpıklık, bir dağılımın simetriden sapma düzeyini ölçen istatistiksel bir göstergedir.Bir dağılım:

• Sağa çarpık (pozitif çarpıklık) olabilir,

• Sola çarpık (negatif çarpıklık) olabilir,

• Ya da sıfır çarpıklığa yakın bir yapıda olabilir.

Dağılımın tepe noktası (mod) referans alınır ve sağ veya sol uçtaki “kuyrukların” uzunluğu çarpıklığın yönünü belirler.

Sıfır Çarpıklık (Simetrik Dağılım)

Bir dağılımın sağ ve sol tarafı birbirinin aynısıysa, sıfır çarpıklığa sahiptir.Bu durumda:

• Ortalama ≈ Medyan

• Dağılım “denge” halindedir.

Simetrik dağılım denilince ilk akla gelen normal dağılımdır, ancak:

• Uniform dağılım,

• Bazı iki tepeli (bimodal) dağılımlar

da simetrik olabilir.

Örnek:

Altı haftalık civciv ağırlıklarının histogramında sağ ve sol tarafın benzer şekilde dağılması, çarpıklığın sıfıra yakın olduğunu gösterir.

Sağa Çarpıklık (Pozitif Çarpıklık)

Sağa çarpık bir dağılımda sağ tarafta uzun bir kuyruk bulunur.

Bu, aşırı yüksek değerlere sahip az sayıdaki gözlem nedeniyle oluşur.

Özellikleri:

• Ortalama > Medyan

• Sağ uçta seyrek ama yüksek değerler vardır.

• İstatistiksel analizlerde modele doğru yaklaşım yapılmazsa “yanıltıcı yüksek ortalama” hissi oluşturabilir.

Örnek:

1749–1983 yılları arasındaki yıllık güneş lekesi sayıları sağa çarpık bir dağılım oluşturur. Bunun nedeni bazı yıllarda gözlenen aşırı yüksek güneş lekesi aktiviteleridir.

Sola Çarpıklık (Negatif Çarpıklık)

Sola çarpıklıkta dağılımın sol tarafında uzun bir kuyruk vardır. Genellikle “çok düşük değerlerin az sayıda olması” durumunda görülür.

Özellikleri:

• Ortalama < Medyan

• Düşük değerlerde seyrek ama uç noktalar bulunur.

Örnek:

Bir zooloji sınavının sonuçlarında çoğu öğrenci yüksek puan alırken çok az sayıda öğrenci çok düşük puan almış olabilir. Bu durumda sınav dağılımı sola çarpık olur.

Çarpıklık Nasıl Hesaplanır? (Pearson’ın Medyan Çarpıklığı)

Verdiğin kaynakta kullanılan ölçü Pearson Median Skewness yöntemidir.

Formülü:

Bu formül, ortalama ve medyan arasındaki farkın standart sapmaya göre kaç birim uzaklıkta olduğunu gösterir.

Örnek:

Güneş lekesi sayıları için:

• Ortalama = 48.6

• Medyan = 39

• Standart sapma = 39.5

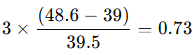
Bu değer pozitif çarpıklığı doğrular.

Çarpık Veri ile Ne Yapılır?

Birçok istatistiksel model (t-testi, ANOVA, regresyon vb.) normal dağılım varsayımı üzerine kuruludur.

Bu nedenle çarpıklık çoğu analizde önemli bir kontrol noktasıdır.

Çarpık veriyle karşılaşıldığında üç seçenek vardır:

1) Hiçbir İşlem Yapmamak

Mild çarpıklık çoğu parametrik testte sorun yaratmaz.

2) Normal dağılıma ihtiyaç duymayan yöntemlere geçmek

• Mann-Whitney U

• Kruskal-Wallis

• Spearman rho

• Genelleştirilmiş Lineer Modeller gibi dağılım serbest yöntemler seçilebilir.

3) Veri dönüşümü yapmak

Sağa çarpıklıkta:

• Hafif → dönüşüm yapma

• Orta → karekök

• Güçlü → doğal log (ln)

• Çok güçlü → log10

Sola çarpıklıkta:

• Önce veri yansıtılır (reflect)

• Sonra aynı dönüşümler uygulanır

Not: Yansıtma işleminde ilişkilerin yönü tersine döner (pozitif korelasyon → negatif).

Pratikte Çarpıklığın Önemi

• Model varsayımlarını kontrol etmek için kullanılır.

• Ortalama yerine medyan kullanılması gerektiğini fark ettirir.

• Dağılımın yapısını anlamak, kutu grafikleri ve istatistiksel raporlamalarda doğru ifadeleri seçmeyi sağlar.

• Veri temizleme ve dönüşüm adımlarının tam olarak nerede ve neden yapılacağını gösterir.

Çarpıklık (Skewness) Sıkça Sorulan Sorular

Normal dağılım nedir?

Normal dağılım, verilerin merkezde yoğunlaştığı ve uçlara doğru gidildikçe azaldığı simetrik bir dağılım türüdür. Sol ve sağ tarafı birbirinin ayna yansımasıdır ve dağılımda hiçbir çarpıklık (skewness) yoktur.

Normal dağılımın temel özelliği nedir?

Normal dağılımın ayırt edici özelliği skewness = 0 olmasıdır. Yani dağılımın her iki tarafı eşit biçimde yayılır ve asimetri bulunmaz.

Normal dağılımda merkezi eğilim ölçümleri nasıl konumlanır?

Normal dağılımda:

• Ortalama (mean)

• Ortanca (median)

• Mod (mode)

tam olarak aynı noktadadır. Bu, dağılımın simetrisinden doğan temel bir özelliktir.

Normal dağılımda uç değerler nasıl davranır?

Merkezden uzaklaştıkça değerlerin sıklığı düzenli biçimde azalır. Uçlardaki değerler nadir görülür ve dağılımın iki tarafı da aynı şekilde “ince kuyruğa” sahiptir.

Normal dağılımın grafik görünümü nasıldır?

Grafik, en yüksek noktasını ortalama üzerinde alan, iki tarafa eşit şekilde yayılan çan şeklinde bir eğridir.

Normal dağılım ile çarpıklık (skewness) arasındaki ilişki nedir?

• Normal dağılım → Skewness = 0

• Sağ çarpık → Skewness > 0

• Sol çarpık → Skewness < 0

Yani normal dağılım, çarpıklığın sıfır olduğu özel bir durumdur.

Gerçek veri setleri her zaman tam normal dağılıma uyar mı?

Gerçek veri çoğu zaman mükemmel şekilde normal dağılmaz. Ancak dağılım yaklaşık simetrik ise pratik açıdan normal olarak kabul edilir.