Uygulamalı SPSS Veri Analizi: Kruskal–Wallis Testi ile Departmanlar Arasında Çalışan Memnuniyet Farklılıklarının İncelenmesi

Kruskal-Wallis testinin uygulamalı bir şekilde çalışmasına geçilmeden önce kısa ve öz teorik bilgilerle test özelliğini hatırlayarak konuya hakim olalım. Bu analiz çalışmasında fark çıkacağı için post-hoc test olarak Mann Whitney U testi ile ikili grup karşılaştırmaları yapacağız.

Kruskal–Wallis Testi Nedir?

Kruskal–Wallis testi, parametrik “Tek Yönlü ANOVA”nın non‑parametrik eşdeğeridir. Üç veya daha fazla bağımsız grubun ölçümlerinin dağılımı hakkında varsayımlar (normal dağılım, varyans homojenliği) sağlanamadığında kullanılır.

Ne İşe Yarar?

• Gruplar Arası Fark Üç veya daha fazla bağımsız grubun puanlarının (ya da gözlem değerlerinin) medyanları yerine sıra ortalamaları (mean rank) üzerinden karşılaştırılmasını sağlar.

• Parametrik Olmayan Alternatif Veriler ordinal ölçekliyse veya sürekli veriler normal dağılım göstermiyor ya da varyanslar eşit değilse ANOVA’nın yerine tercih edilir.

Hangi Durumlarda Kullanılır?

1. Bağımsız Üç Grup

   • Örneğin, A, B ve C departmanlarının memnuniyet skorlarını karşılaştırmak.

2. Ölçüm Ölçeği

   • Veriler en az ordinal (sıralama) ölçekli olmalıdır.

3. Varsayımların Sağlanmaması

   • Veri dağılımı normal değilse veya Levene testi ile saptanan varyans homojenliği sağlanmıyorsa.

4. Küçük Örneklemler

   • Her bir grubun örneklem sayısı ≥ 5–10 kişi olduğunda testi uygulamak hâlâ geçerlidir.

Testin Mantığı ve İşleyişi

1. Tüm Gözlemlerin Birleştirilmesi ve Sıralanması

   • Üç grubun tüm puanları tek bir listede küçükten büyüğe sıralanır.

   • Eşit değerler varsa “ortalama sıra” (mid‑rank) verilir.

2. Gruplar İçin “Mean Rank” Hesaplama

   • Her gözleminin ait olduğu grubun sıra ortalamasına (mean rank) bakılır.

3. H‑İstatistiği (Chi‑Square Yaklaşımı)

   • Gruplar arası mean rank farklarının büyüklüğü, χ² benzeri bir H değeriyle ölçülür.

4. p‑Değeri ile Karar

   • H₀: “Tüm grupların dağılımları aynıdır.”

   • H₁: “En az iki grubun dağılımı farklıdır.”

   • Eğer p < 0.05, H₀ reddedilir → gruplar arasında anlamlı fark var.

Testin Çıktıları ve Yorum

• Chi‑Square (H) Değeri: SPSS’te “Chi‑Square” ya da “H” olarak raporlanır.

• df: Serbestlik derecesi = (grup sayısı − 1).

• Asymp. Sig.: p‑değeri; < 0.05 ise gruplar arası fark vardır.

• Post‑Hoc Analiz: Fark bulunduysa hangi grupların farklılaştığını belirlemek için Mann–Whitney U (Bonferroni düzeltilmiş) gibi çiftler arasında testler uygulanır.

Özet

• Kullanım: Üç veya daha fazla bağımsız grubun sıralama verilerini karşılaştırmak.

• Avantaj: Normal dağılım veya varyans homojenliği varsayımlarını gerektirmez.

• Sonuç: H değeri ve p‑değeri ile “gruplar arasında fark var mı?” sorusunu yanıtlar; gerekirse post‑hoc testlerle “hangi gruplar farklı?” saptanır.

Aşağıdaki dosya indirme bağlantısından uygulamalı Kruskal-Wallis testi için kullanılan veri setini indirebilir ve inceleyebilirsiniz.

Kruskal_Wallis_Analizi_Departman_Memnuniyet_Veri_Seti.csv

CSV dosyasını indir • 567B

Aşağıdaki tablo, SPSS yazılımda değişkenlerin Variable View sekmesinde tanımlanmasının nasıl oluşturulduğunu anlatmak için eklenmiştir.

Name	Type	Width	Decimals	Label	Values	Missing	Columns	Align	Measure	Role
Departman	Numeric	8	0	Çalışanın Çalıştığı Departman	1 = Muhasebe , 2 = Pazarlama , 3 = Üretim	—	8	Right	Nominal	Input
Memnuniyet_Puani	Numeric	8	1	Çalışan Memnuniyet Puanı (1-10)	—	—	8	Right	Scale	Input

Aşağıdaki görsel ise veri setine ait değişkenlerin SPSS yazılımında Variable View sekmesinde tanımlamasına aittir.

SPSS yazılımında Kruskal–Wallis Testi'nin nasıl yapıldığını tekrar hatırlayalım:

1- Analyze, Nonparametric Tests, Legacy Dialogs, K Independent Samples seçilir.

2- Test for Several Independent Samples penceresinde sol taraftaki değişken listesinden bağımlı nicel değişken Test Variable List’e taşınır.

3- Sol taraftaki değişkenler listesinden bağımsız kategorik değişken seçilerek sağ taraftaki Grouping Variable kısmına aktarılır.

4- Define Range tıklanır ve bağımsız değişken kategorilerinin aralığı (hangi kod aralığında olduğu) yazılır ve Continue tıklanır.

5- Two Independent Samples Test penceresinde Kruskal-Wallis Test H testi otomatik seçilidir. OK Tıklanır.

Bir sonraki aşamaya geçelim. Oluşturduğumuz veri seti ile Kruskal-Wallis analizini uygulamalı olarak gerçekleştirelim ve birlikte analiz edelim.

Tablo 1: Kruskal-Wallis Test - Ranks

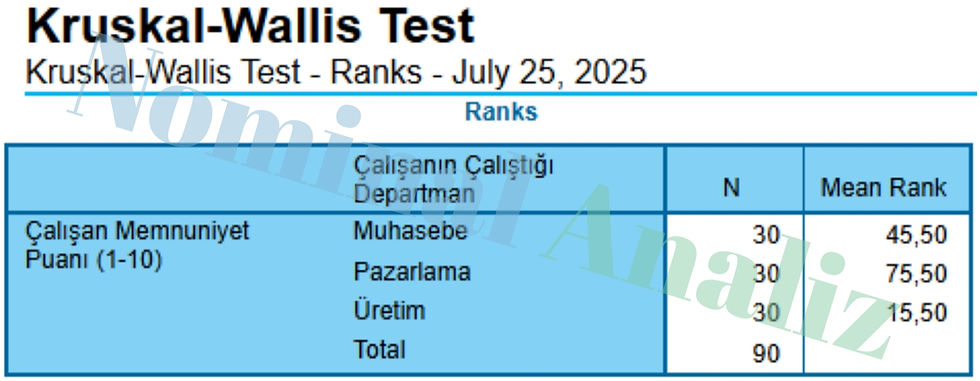
• Her grubun (departmanın) örneklem büyüklüğü eşit: Analize her departmandan 30 çalışan dahil edilmiş.

• Mean Rank (Sıra Ortalaması):

  • Pazarlama departmanı: Sıra ortalaması en yüksek (75,50)

  • Muhasebe departmanı: Orta düzeyde (45,50)

  • Üretim departmanı: En düşük sıra ortalamasına sahip (15,50)

Ne Anlama Gelebilir?

• Sıra ortalaması bir grubun genel olarak “veri dağılımında üst sıralarda mı, alt sıralarda mı” yer aldığını gösterir.

• Pazarlama departmanı çalışanları, memnuniyet puanları açısından en yüksek sırada yer almaktadır. Yani, bu grubun çalışanlarının memnuniyet puanları genellikle daha yüksektir.

• Muhasebe departmanı çalışanlarının memnuniyet puanları, üç departman arasında ortalama seviyededir.

• Üretim departmanı ise, memnuniyet puanları bakımından en alt sıradadır; yani çalışanların memnuniyet puanları diğer iki departmana göre daha düşüktür.

• Bu bulgular, departmanlar arasında çalışan memnuniyeti bakımından farklılıklar olabileceğine işaret eder.

Tablo 2: Kruskal-Wallis Test - Test Statistics

• Kruskal-Wallis H değeri, gruplar arasındaki sıra ortalamalarının birbirinden ne kadar farklı olduğunu ölçer.

• df (serbestlik derecesi), karşılaştırılan grup sayısının bir eksiğidir.

• Asymp. Sig. (p değeri), gruplar arasında anlamlı bir fark olup olmadığını gösterir.

• Burada p değeri ,000 olarak verilmiş; yani p < 0,05 (hatta < 0,001) olduğu için, gruplar (departmanlar) arasında istatistiksel olarak anlamlı bir fark vardır.

Sonuç

• Departmanlara göre çalışan memnuniyet puanları arasında anlamlı farklılık vardır.

• Hangi departmanların birbirinden farklı olduğunu görmek için post-hoc (ör. Mann-Whitney U) testlerine başvurmak gerekir.

Fark çıktığı için post-hoc test olarak Mann Whitney U testi ile ikili grup karşılaştırmaları yapıyoruz.

SPSS Uygulaması:

1- Analyze, Nonparametric Tests, Legacy Dialogs, 2 Independent Samples seçilir.

2- Two Independent Samples Test penceresinde Sol taraftaki değişken listesinden bağımlı nicel değişken Test Variable List’e taşınır.

3- Sol taraftaki değişkenler listesinden bağımsız kategorik değişken seçilerek sağ taraftaki Grouping Variable kısmına aktarılır.

4- Define Groups tıklanır ve bağımsız değişken kategorilerinin ne olarak kodlandığı yazılır ve Continue tıklanır.

5- Two Independent Samples Test penceresinde Test Type Mann-Whitney U testi otomatik seçilidir.

6- OK Tıklanır.

Bu uygulamayı/karşılaştırmayı bu örnek için 3 kez yapıyoruz: 1. Grup-2. Grup karşılaştırması, 1. Grup-3. Grup karşılaştırması ve 2. Grup-3. Grup karşılaştırması için.

Karşılaştırma Çıktısı 1 (1. Grup - 2. Grup)

Karşılaştırma Çıktısı 2 (1. Grup - 3. Grup)

Karşılaştırma Çıktısı 3 (2. Grup - 3. Grup)

• Her karşılaştırmada Mann-Whitney U değeri 0,000 ve p değeri ,000 olarak görülmektedir.

• p < 0,05 (hatta < 0,001) olduğu için, her iki grup arasında istatistiksel olarak anlamlı bir fark bulunmaktadır.

• Sıra ortalamalarına bakıldığında, sıralama açısından her ikili karşılaştırmada gruplardan biri açıkça diğerine üstün gelmektedir.

• Bu bulgular, her üç grup arasında da (Muhasebe–Pazarlama, Muhasebe–Üretim, Pazarlama–Üretim) çalışan memnuniyet puanlarının istatistiksel olarak anlamlı şekilde farklılık gösterdiğini gösterir.

Not: Yorumun doğruluğu için, çoklu karşılaştırmalarda hata oranını kontrol etmek adına Bonferroni düzeltmesi uygulanmalıdır (3 test için 0,05/3 ≈ 0,017; buradaki tüm p değerleri bu sınırın altında).

Departmanlara Göre Çalışan Memnuniyet Puanlarının Karşılaştırılması

Departman	n	Sıra Ortalaması	Kruskal-Wallis H	df	p	Anlamlı Fark*
Muhasebe	30	45,50				Muhasebe – Pazarlama
Pazarlama	30	75,50	79,305	2	,000	Muhasebe – Üretim
Üretim	30	15,50				Pazarlama – Üretim
Toplam	90

* Mann-Whitney U testi yapılmıştır. Bonferroni düzeltmesi sonrası p < 0,0167 düzeyinde anlamlı fark çıkan sonuçlar gösterilmiştir.

Araştırma grubundaki departmanlara göre çalışanların memnuniyet puanı sıra ortalaması:

• Muhasebe: 45,50

• Pazarlama: 75,50

• Üretim: 15,50

Departmanlar arasında çalışan memnuniyeti puanlarının sıra ortalamaları arasında istatistiksel olarak anlamlı bir farklılık tespit edilmiştir (Kruskal-Wallis H = 79,305, df = 2, p < 0,001).

Etki Büyüklüğü Hesabı (Eta Kare, η²):

Eta kare = H / (n – 1)Eta kare = 79,305 / (90 – 1) Eta kare ≈ 0,89

• Eta kare (η²) = 0,89 (Çok büyük etki)

• Bu sonuç, toplam varyansın %89’unun bağımsız değişken olan “departman” tarafından açıklandığını göstermektedir.

Farkın Kaynağı

Farklılığın, Muhasebe ile Pazarlama, Muhasebe ile Üretim ve Pazarlama ile Üretim departmanlarının sıra ortalamalarının birbirinden farklılaşmasından kaynaklandığı tespit edilmiştir (Mann-Whitney U testleri, p < 0,001).

Bonferroni düzeltmesi sonrası yapılan ikili karşılaştırmalarda, her üç eşleşmede de anlamlı fark bulunmuştur (anlamlılık sınırı: p < 0,0167).

Analiz Sonucu

Departmanlar arasında çalışan memnuniyet puanlarında büyük ve anlamlı farklılıklar vardır. Fark, özellikle Pazarlama departmanının en yüksek, Üretim departmanının ise en düşük memnuniyet sıra ortalamasına sahip olmasından kaynaklanmaktadır.

Analiz bulguları, çalışan memnuniyetinin departmana göre anlamlı biçimde değiştiğini göstermektedir.

Aşağıdaki dosya indirme bağlantısından uygulamalı veri analizi çalışmasından elde edilen SPSS çıktısını indirebilir ve inceleyebilirsiniz.

Kruskal_Wallis_Analizi_Departman_Memnuniyet_Veri_Seti_Kullanilarak_Uygulamali_Veri_Analizi.

dosyasını indir • 179KB