Uygulamalı Finansal Veri Analizi: Tek Yönlü ANOVA ile Düşük, Orta ve Yüksek Risk Gruplarının Getiri Oranlarının Karşılaştırılması

Uygulamalı "Tek Yönlü ANOVA" testine başlamadan önce kısa ve öz teorik bilgilerle testin özelliğini hatırlayalım. Bu çalışmanın en önemli noktası "One‑Way ANOVA’nın standart varsayımlarından birinin ihlal edilmesi olacaktır. Bu hatayı birlikte tespit edeceğiz, veri seti varyansı homojen olmadığı için "Post-Hoc yöntemlerinden olan "Games-Howell" yöntemini kullanıp, tekrar değerlendirmeye alacağız.

Tek Yönlü ANOVA (One‑Way ANOVA) Nedir? Tek Yönlü ANOVA, üç veya daha fazla bağımsız grubun ortalamaları arasında istatistiksel olarak anlamlı fark olup olmadığını test eden parametrik bir yöntemdir.

Ne İşe Yarar?

• Ortalamalar Arası Karşılaştırma: Bir bağımsız (faktör) değişkenin üç ve üzeri kategorisinin (örneğin “düşük/orta/yüksek risk”) bağımlı değişken (örneğin getiri oranı) üzerindeki etkisini sınar.

• Varyans Analizi: “Gruplar arası” ve “gruplar içi” varyansı karşılaştırarak F‑istatistiğini hesaplar; yüksek F değeri → grup ortalamaları arasında anlamlı fark.

Hangi Durumlarda Kullanılır?

1. Bağımsız Gruplar: Gruptaki katılımcılar birbirinden bağımsızsa (ör. farklı yatırım stratejisi uygulayan portföyler).

2. En Az Aralık Ölçeği: Bağımlı değişken niceliksel (ör. getiri yüzdeleri), sürekli veya yaklaşık sürekli.

3. Normal Dağılım Varsayımı: Her grubun ölçümleri yaklaşık normal dağılmış olmalı (veya örneklem boyutları yeterince büyük ≥ 30).

4. Varyans Homojenliği (Opsiyonel): Gruplar arası varyanslar eşitse ideal, değilse robust test veya Welch ANOVA tercih edilir.

Aşağıdaki dosya indirme bağlantısından bu uygulamalı çalışmada kullanılan veri setini CSV formatında indirebilir ve inceleyebilirsiniz.

One-Way_ANOVA_Uygulamali_Veri_Analizi_Finansal_Veri_Seti.csv

CSV dosyasını indir • 1KB

Aşağıdaki tabloda ise SPSS yazılımında Variable View sekmesinde değişkenlerin nasıl tanımlandığı/ayarlandığı yer almaktadır.

Name	Type	Width	Decimals	Label	Values	Missing	Columns	Align	Measure	Role
RiskKod	Numeric	8	0	Risk Grubu Kodu	1 = Düşük Risk 2 = Orta Risk 3 = Yüksek Risk	None	8	Right	Ordinal	Input
YillikGetiri	Numeric	8	2	Yıllık Getiri Oranı (%)	—	None	8	Right	Scale	Input

Aşağıdaki görsel, veri setinin SPSS yazılımında Variable View sekmesinde değişken tanımlamasına aittir.

SPSS yazılımında "Tek Yönlü ANOVA" testinin nasıl yapıldığını tekrar hatırlayalım:

1- Analyze, Compare Means, One-way ANOVA seçilir.

2- One-way ANOVA penceresinde sol taraftaki değişkenler listesinden nicel değişkenler seçilerek sağ taraftaki Dependent List kutusuna aktarılır. Sol taraftaki değişkenler listesinden kategorik (bağımsız) değişken seçilerek sağ taraftaki Factor kutusuna aktarılır.

3- One-way ANOVA penceresinde Options tıklanır ve Desciriptive Homogeneity of variance test seçilir. Continue tıklanır.

4- One-way ANOVA penceresinde (ANOVA testinde fark çıkar ise) Post-Hoc tıklanır ve Varyanslar eşit ise Equal Variances Assummed kısmından bir test seçilir. Varyanslar eşit değil ise Equal Variances Not Assummed kısmından bir test seçilir. Continue tıklanır.

5- One-way ANOVA penceresinde OK tıklanır.

Şimdi aşamada Tek Yönlü ANOVA testinin analiz sonuçlarını adım adım yorumlayalım.

Tablo 1: Oneway - Descriptives

1. Örneklem Büyüklüğü (N)

   • Her risk grubunda eşit sayıda yatırımcı var (Düşük Risk = 20, Orta Risk = 20, Yüksek Risk = 20; toplam 60).

   • Bu, ANOVA varsayımı olan “gruplar arası örneklem büyüklüklerinin eşit olması” koşulunu sağlamaya yardımcı olur.

2. Ortalama (Mean)

   • Düşük Risk: % 4,83

   • Orta Risk: % 8,18

   • Yüksek Risk: % 14,90

   • Ortalama getiriler, risk seviyesi yükseldikçe artıyor; bu da “daha yüksek risk – potansiyel olarak daha yüksek getiri” ilişkisini gösteriyor.

3. Standart Sapma (Std. Deviation)

   • Düşük Risk: 1,23

   • Orta Risk: 2,04

   • Yüksek Risk: 3,31

   • Risk grubu yükseldikçe getirilerin dağılımı da genişliyor; yüksek risk grubunda yatırımların performansı daha değişken.

4. Standart Hata (Std. Error)

   • Düşük Risk: 0,28

   • Orta Risk: 0,46

   • Yüksek Risk: 0,74

   • Ortalama tahminlerinin güvenilirliği, grup büyüklüğünün aynılığına rağmen risk yükseldikçe biraz azalıyor (daha büyük sapma → daha yüksek hata).

5. %95 Güven Aralığı (95% CI for Mean)

   • Düşük Risk: [4,25, 5,41]

   • Orta Risk: [7,23, 9,14]

   • Yüksek Risk: [13,35, 16,45]

   • Bu aralıklar hemen hemen çakışmıyor; gruplar arası ortalama farklarının anlamlı olabileceğine dair ilk işareti verir.

6. Minimum ve Maksimum Değerler

   • Düşük Risk: 3,08 – 6,88

   • Orta Risk: 5,33 – 11,76

   • Yüksek Risk: 10,34 – 19,70

   • En düşük risk grubunda bile aylık getiri %3 civarına düşebiliyor; yüksek risk grubunda ise bazen %20’ye yakın kazanç görülebiliyor.

Sonuç

• Risk seviyesi yükseldikçe ortalama getiri ve veri dağılımı (standart sapma) artıyor.

• %95 güven aralıklarının büyük ölçüde ayrışması, gruplar arası farkların ANOVA ile sınanması gerektiğine işaret ediyor.

Tablo 2: Oneway - Test of Homogeneity of Variances

1. Test Amacı Levene testi, üç risk grubundaki “Yıllık Getiri Oranı” değişkeninin varyanslarının birbirine eşit olup olmadığını sınar.

2. Test İstatistiği ve Anlamlılık (Sig.)

   • Based on Mean: Levene = 12,584; df1 = 2; df2 = 57; p = .000

   • Based on Median: Levene = 12,204; df1 = 2; df2 = 57; p = .000

   • (Diğer uyarlamalı hesaplamalar da aynı sonuçta p = .000)

3. Karar Tüm varyans homojenliği kriterlerinde p < .05 olduğu için (p ≈ 0,000), gruplar arası varyanslar eşit değildir.

4. Ne Yapmalıyız?

   • One‑Way ANOVA’nın standart varsayımlarından biri ihlal oldu.

   • Klasik ANOVA yerine Welch ANOVA (varyans eşitsizliğine dayanıklı) veya normal ANOVA’yı kullanacaksak Games‑Howell gibi “homojen olmayan varyanslar” için uygun post‑hoc yönteme yönelmeliyiz.

Sonraki Adım:

Bu çıktıyı geçerli kılmak için şimdi ANOVA (veya Welch ANOVA) tablosunu inceleyip, gruplar arası farkın anlamlı olup olmadığını ve ardından Games‑Howell post‑hoc sonuçlarını yorumlayacağız.

Aşağıdaki görsel varyans homejenliği sağlanamadığı için post-hoc yöntemlerinden biri olan Games-Howell yönteminin SPSS yazılımında uygulanmasına aittir.

Tablo 3: Oneway - ANOVA

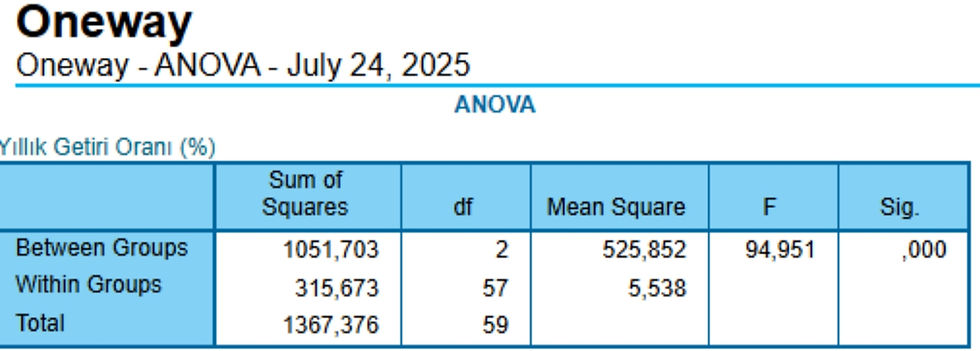
• Kayıp Kareler (Sum of Squares)

  • Between Groups (Gruplar Arası): 1051,703

    • Risk grupları arasındaki “Yıllık Getiri” farkının yarattığı toplam varyans.

  • Within Groups (Gruplar İçi): 315,673

    • Aynı risk grubundaki bireyler arasındaki rastgele varyans.

  • Total (Toplam): 1367,376

    • Hem grup içi hem de grup arası varyansın toplamı.

• Serbestlik Dereceleri (df)

  • Between Groups: df₁ = k–1 = 3–1 = 2 (üç risk grubu → iki serbestlik)

  • Within Groups: df₂ = N – k = 60–3 = 57

  • Total: dfₜ = N – 1 = 60–1 = 59

• Kareler Ortalaması (Mean Square)

  • Between Groups: MS₁ = SS₁/df₁ = 1051,703 / 2 = 525,852

  • Within Groups: MS₂ = SS₂/df₂ = 315,673 / 57 = 5,538

• F İstatistiği ve Anlamlılık

  • F(2, 57) = 525,852 / 5,538 ≈ 94,951

  • Sig. = .000 (p < .001) → Risk grupları arasında yıllık getiri oranı ortalamaları istatistiksel olarak anlamlı biçimde farklı.

• Pratik Önemi: Etki Büyüklüğü (Eta Kare)

  • η² = SS_between / SS_total = 1051,703 / 1367,376 ≈ 0,769

  • Yani, %77’lik devasa bir varyans payı risk grubuna (düşük/orta/yüksek) bağlanabiliyor. Bu da “grubun getiriye etkisinin” çok güçlü olduğunu gösterir.

• Ne Anlamalıyız?

  • Düşük, Orta ve Yüksek Risk gruplarının yıllık getiri ortalamaları arasında çarpıcı derecede fark var.

  • Homojenlik varsayımı Levene testiyle (p = .000) ihlal edilmiş olsa da, ANOVA yine de bu ayrımı saptadı; post‑hoc’ta Games–Howell ile hangi grupların birbirinden ayrı ayrı farklılaştığına bakacağız.

Tablo 4: Post Hoc Tests - Multiple Comparisons

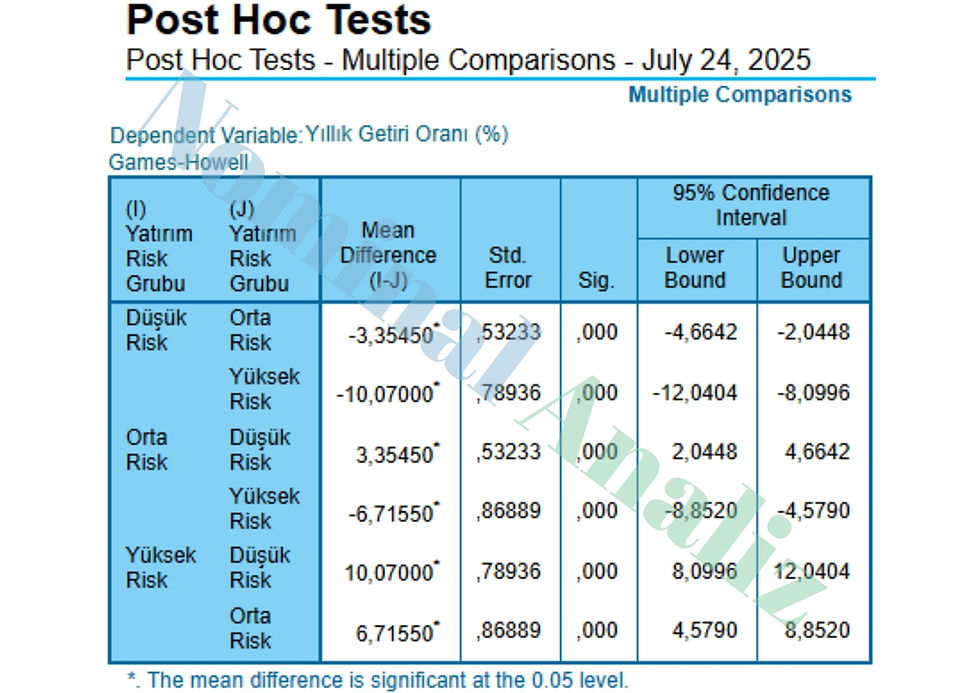
1. Düşük Risk – Orta Risk

   • Ortalamalar Arasındaki Fark (Düşük – Orta): –3,3545 (%)

   • p = .000 → Bu fark istatistiksel olarak çok anlamlı.

   • %95 Güven Aralığı: [–4,6642; –2,0448]

   • Yorum: Orta risk grubunun yıllık getirisi, düşük risk grubuna göre ortalama 3,35 puan daha yüksek.

2. Düşük Risk – Yüksek Risk

   • Ortalamalar Arasındaki Fark (Düşük – Yüksek): –10,0700 (%)

   • p = .000 → Son derece anlamlı.

   • %95 Güven Aralığı: [–12,0404; –8,0996]

   • Yorum: Yüksek risk grubunun getirisi, düşük risk grubuna göre ortalama 10,07 puan daha yüksek.

3. Orta Risk – Yüksek Risk

   • Ortalamalar Arasındaki Fark (Orta – Yüksek): –6,7155 (%)

   • p = .000 → Anlamlı.

   • %95 Güven Aralığı: [–8,8520; –4,5790]

   • Yorum: Yüksek risk grubunun getirisi, orta risk grubuna göre ortalama 6,72 puan daha yüksek.

4. Tüm Diğer Karşılaştırmalar

   • “(J)–(I)” biçimindeki ters yönlü farklar da aynı sonuçları yansıtır (örneğin, Orta–Düşük = +3,3545, Yüksek–Düşük = +10,07, Yüksek–Orta = +6,7155).

Genel Değerlendirme:

• Tüm çiftler arası karşılaştırmalar (Düşük–Orta, Düşük–Yüksek, Orta–Yüksek) p < .001 düzeyinde anlamlı.

• Yüksek Risk grubu, en yüksek yıllık getiriyi (≈14,9 %) sağlarken;

• Orta Risk grubu ortalama ≈8,18 %,

• Düşük Risk grubu ise ortalama ≈4,83 % getiri elde etmiş.

• Bu üç grup arasında her bir eşleşme için güven aralıklarının sıfır içermemesi, farkların tutarlı ve güçlü olduğunu gösterir.

Sonuç: Finansal risk grubu arttıkça ortalama getiri de anlamlı biçimde artıyor. Bu da “risk–getiri” ilişkisinin hem istatistiksel hem de pratik açıdan belirgin olduğunu teyit ediyor.

Aşağıdaki dosya indirme butonundan uygulamalı veri analizi çalışması için elde edilen SPSS çıktısını indirebilir ve inceleyebilirsiniz.

One Way ANOVA Uygulamalı Veri Analizi Finansal Veri Seti SPSS Çıktısı Post Hoc Testi Yapıl.

dosyasını indir • 211KB