SPSS Uygulamalı Analiz: Keşfedici Faktör Analizi (EFA) — Hava Kirliliği (ABD Şehirleri) Veri Seti

Aşağıdaki çerçeve, SPSS’te uygulamalı faktör analizi yapmadan önce referans alacağımız kısa ve öz “ön bilgi” paketidir. Analiz türü (EFA) ve kullanacağımız veri seti (ABD hava kirliliği: X1–X6) vurgulanmıştır.

Nedir?

• Keşfedici Faktör Analizi (EFA), çok sayıdaki gözlenen değişkenin (X1–X6) ortak varyansını açıklayan daha az sayıda gizil faktör ile özetlenmesini amaçlar.

• Amaç: boyut indirgeme, yapı keşfi, değişkenleri anlamlı kümeler/faktörler altında toplama.

Ne Zaman Uygulanır?

• Değişkenler arasında anlamlı korelasyonlar varsa (örn. iklim ve yağış göstergeleri birlikte değişiyor).

• Ölçek geliştirme, endeks oluşturma veya çok değişkenli yapıyı sadeleştirme ihtiyacı olduğunda.

• Modeli keşfetmek istediğimizde (önceden belirlenmiş faktör yapısı yoksa).

Uygulama Koşulları ve Gereklilikler

• Veri seti (bu çalışmada): ABD’nin 41 şehrine ait çevresel değişkenler (X1: sıcaklık, X2: imalat işletmeleri, X3: nüfus, X4: rüzgâr hızı, X5: yıllık yağış, X6: yağışlı gün sayısı).

  • Analizde kullanılacak değişkenler: X1–X6 (Y = SO₂ düzeyi, faktör analizinde “faktörlenmeyecek” hedef değişken; daha sonra faktör skorlarıyla ilişki için kullanılabilir).

• Ölçek farkı olduğundan korelasyon matrisi üzerinden çalışmak ve standartlaştırma (Z-skor) tercih edilir.

• Örneklem yeterliği: Değişken başına en az 5–10 gözlem önerilir; n=41 ve p=6 için makul.

• Faktörlenebilirlik testleri:

  • KMO ≥ 0.60 (tercihen ≥ 0.70)

  • Bartlett küresellik testi p < 0.05

• Çoklu bağlantı aşırı olmamalı (değişkenlerin birbirinin neredeyse kopyası olmaması).

• Aykırı değerler ve eksik değerler kontrol edilmeli.

Önemli Bilgiler (Yöntem, Karar Kuralları, SPSS Seçimleri)

• Çıkarma (Extraction):

  • Principal Axis Factoring (PAF): Ortak varyansı hedefler; dağılım varsayımı daha esnek.

  • Maximum Likelihood (ML): Çok değişkenli normallik varsayar; faktör sayısı için uyum testi sağlar.

• Faktör Sayısı Belirleme:

  • Özdeğer > 1 (Kaiser), Scree Plot “dirsek”, Paralel Analiz (tercihen).

• Rotasyon:

  • Varimax (ortogonal): Bağımsız faktörler, yorum kolaylığı.

  • Promax/Oblimin (oblik): Faktörler arası korelasyona izin verir; gerçekçi yapılar için faydalı.

• Yükler (Loadings) & Komünalite:

  • |yük| ≥ 0.40 genelde anlamlı kabul edilir (bağlama göre).

  • Komünalite yüksekse değişken faktörlerce iyi açıklanır.

• Faktör Skorları:

  • SPSS’te “Save as variables” ile kaydedilip Y (SO₂) ile korelasyon veya regresyon analizinde kullanılabilir (istenen egzersizin temel adımı).

• Raporlama:

  • KMO, Bartlett; çıkarma yöntemi; faktör sayısı gerekçesi; rotasyon türü; döndürülmüş faktör yükleri; komünaliteler; açıklanan toplam varyans; faktör skorları ile Y arasındaki korelasyonlar ve dağılım grafiği (scatterplot).

Uygulamalı ‘Faktör Analizi’ çalışmamızda kullanılan hava kirliliği veri setine aşağıdaki dosya indirme bağlantısından erişebilir ve inceleyebilirsiniz.

SPSS Uygulamalı Faktör Analizi Veri Seti Hava Kirliliği.csv

CSV dosyasını indir • 2KB

SPSS Uygulamalı: Hava Kirliliği Veri Seti ile Faktör Analizi (EFA) Adım Adım Rehber

1. Veri Setini SPSS’e Aktarma

• File > Open > Data yolunu izleyerek hazırladığın CSV dosyasını (Y, X1–X6 değişkenleri) SPSS’e aktar.

• Variable View sekmesinde:

  • Y değişkenini “Scale” (ölçek) olarak bırak (hava kirliliği SO₂ değeri).

  • X1–X6 değişkenlerini de “Scale” olarak seç.

  • Şehir adını tanımladıysan “Nominal” olarak işaretle ve “Label Cases by” için kullanılacak şekilde ayarla.

2. Faktör Analizine Başlamak

• Menüden Analyze > Dimension Reduction > Factor… seç.

• Açılan pencerede X1–X6 değişkenlerini seçip Variables kutusuna aktar.

• Descriptives… butonuna tıkla ve KMO ve Bartlett’s Test of Sphericity ile Correlation Matrix kutularını işaretle → Continue.

3. Extraction (Çıkarma Yöntemi) Ayarları

• Extraction… butonuna tıkla:

  • Method: “Principal Axis Factoring” (veya Maximum Likelihood, senin seçimine bağlı).

  • Analyze: “Correlation Matrix” (veriler farklı ölçeklerde olduğu için).

  • Display: “Unrotated Factor Solution” ve Scree Plot kutularını işaretle.

  • Number of Factors: Başlangıçta “Eigenvalue > 1” seçeneğini bırak veya kendin “2” veya “3” olarak belirle.

  • Continue ile çık.

4. Rotasyon Ayarları

• Rotation… butonuna tıkla:

  • Method: Varimax (faktörler bağımsız olsun).

  • Loading Plot(s): İstersen yükleme grafiğini göster.

  • Continue.

5. Faktör Skorlarını Kaydetme

• Ana pencereye dön → Scores… butonuna tıkla:

  • “Save as Variables” kutusunu işaretle.

  • SPSS her şehir için FAC1_1, FAC2_1… gibi faktör skorları oluşturur.

  • Continue.

6. Analizi Çalıştırma

• OK butonuna tıkla.

• SPSS çıktısı:

  • KMO ve Bartlett testi: Faktörlenebilirlik.

  • Communalities: Değişkenlerin ortak varyansları.

  • Total Variance Explained: Faktörlerin açıkladığı toplam varyans yüzdeleri.

  • Rotated Component Matrix: Hangi değişkenin hangi faktöre yüksek yüklendiğini gösterir.

7. Faktör Skorlarını Y ile İlişkilendirme

• Menüden Analyze > Correlate > Bivariate… seç.

• Variables kutusuna Y ve FAC1_1, FAC2_1 skorlarını at.

• Pearson Correlation kutusunu işaretle → OK.

• SPSS sana faktör skorları ile hava kirliliği seviyesi (Y) arasındaki korelasyonu verir.

8. Şehirlerin Faktör Düzleminde Görselleştirilmesi

• Menüden Graphs > Chart Builder > Scatter/Dot seç.

• Simple Scatter seçeneğini ekrana sürükle.

• Y Axis = FAC1_1, X Axis = FAC2_1 seç.

• Label Cases by için şehir değişkenini seç.

• OK butonuna bas.

• Grafik üzerinde şehirleri (case label) görüp hangi şehirlerin benzer hava kirliliği desenlerine sahip olduğunu görebilirsin.

9. Sonuçların Yorumlanması

• Faktör yükleri ≥ 0.40 olan değişkenler o faktör altında toplanır.

• Faktör 1 genellikle hava kirliliği yoğunluğu ile ilgili genel boyutu temsil eder.

• Faktör 2 farklı iklim/yağış dinamiklerini temsil edebilir.

• Y değişkeni ile faktör skorlarının korelasyonu şehirlerin hava kirliliği düzeyine göre ayrışmasını açıklar.

Gerekli tüm ayarlamaları tamamladıktan sonra, elimizdeki hava kirliliği veri seti üzerinde faktör analizi uygulamasını gerçekleştirerek sonuçları birlikte inceleyip özgün bir şekilde yorumlayacağız.

SPSS Uygulamalı Faktör Analizi – KMO ve Bartlett Testi Sonuçları (Hava Kirliliği Veri Seti)

1. KMO (Kaiser-Meyer-Olkin Measure of Sampling Adequacy = 0.365)

• KMO değeri, veri setinin faktör analizi için uygunluğunu gösterir.

• 0.365 değeri oldukça düşük (0.50’nin altında); bu durum değişkenler arası ortak varyansın zayıf olduğunu ve faktör analizinin sınırlı güvenilirlikte olacağını gösteriyor.

• Yorum: Veri setindeki X1–X6 değişkenleri arasında faktör analizi için yeterli korelasyon ağı oluşturulmamış olabilir. Daha fazla değişken eklemek veya veriyi dönüştürmek gerekebilir.

2. Bartlett’s Test of Sphericity (Approx. Chi-Square = 159.231; df = 15; Sig. = 0.000)

• Bartlett testi, korelasyon matrisinin birim matris (değişkenler arası korelasyon yok) olup olmadığını test eder.

• p < 0.001 (Sig. = 0.000) olduğundan sıfır hipotezi reddedilir; yani değişkenler arasında anlamlı korelasyonlar mevcut.

• Yorum: Bu, değişkenler arasında faktör analizine temel oluşturabilecek ilişkilerin bulunduğunu gösterir.

3. Genel Değerlendirme:

• Bartlett testi anlamlı, ancak KMO düşük olduğundan faktör analizi teknik olarak yapılabilir ama elde edilecek faktör yapısının güvenilirliği zayıf olabilir.

• Çözüm önerisi:

  • Değişken sayısını artırmak veya korelasyon yapısını güçlendirecek farklı ölçümler eklemek.

  • Alternatif olarak “Principal Component Analysis” ile boyut indirgeme yapmak.

  • KMO’yu yükseltmek için uygun dönüşümler veya daha homojen değişkenler kullanmak.

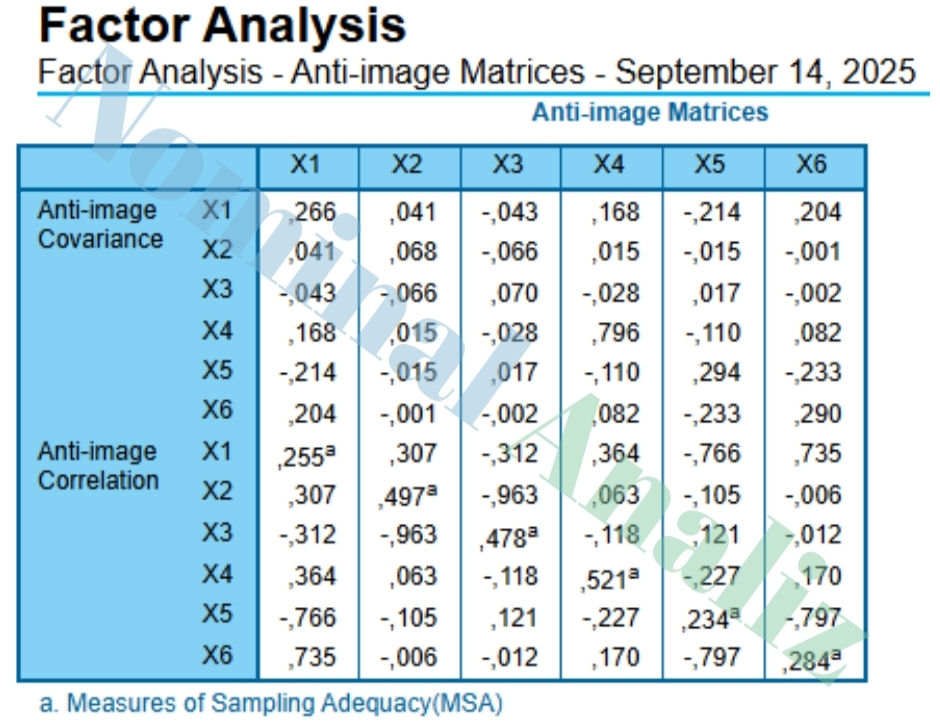
SPSS Uygulamalı Faktör Analizi – Anti-Image Matrisleri (MSA Değerleri)

Yorum:

• Anti-image Correlation kısmındaki diyagonal değerler (MSA) her değişkenin faktör analizine uygunluğunu gösterir.

• MSA ≥ 0.50 olması ideal; 0.30–0.50 arası sınırlı, 0.30’un altı uygun değil.

Tablodan bakarsak:

• X1 = 0.255, X2 = 0.497, X3 = 0.478, X4 = 0.521, X5 = 0.234, X6 = 0.284

• Yalnızca X4 (0.521) 0.50’nin üzerinde, diğerlerinin hepsi düşük veya sınırda.

Sonuç:

• Bu MSA değerleri faktör analizinin veri seti için çok sınırlı uygunlukta olduğunu gösteriyor.

• Özellikle X1, X5, X6 çok düşük MSA değerlerine sahip; bu değişkenler faktör analizinden çıkarılarak yeniden denenebilir.

SPSS Uygulamalı Faktör Analizi – Communalities (Ortak Varyanslar)

Yorum:

• Initial sütunu tüm değişkenlerin başlangıçta %100 varyansla modele girdiğini gösterir.

• Extraction sütunu her değişkenin varyansının ne kadarının faktörler tarafından açıklandığını gösterir.

Tabloda:

• X1 = 0.892, X2 = 0.968, X3 = 0.979, X5 = 0.941, X6 = 0.888 → Yüksek açıklanan varyans (%88–%98 arası)

• X4 = 0.424 → Çok düşük açıklanan varyans (%42), yani faktörler X4’ü zayıf açıklıyor.

Sonuç:

• X1, X2, X3, X5 ve X6 faktör yapısı tarafından güçlü şekilde açıklanıyor.

• X4 değişkeni faktör analizine zayıf uyum sağlıyor; faktör yapısını bozabilir veya ayrı değerlendirilmesi gerekebilir.

SPSS Uygulamalı Faktör Analizi – Toplam Açıklanan Varyans (Total Variance Explained)

Yorum:

• Initial Eigenvalues kısmı, her bileşenin (component) orijinal varyansı ne kadar açıkladığını gösterir.

• Extraction Sums of Squared Loadings kısmı, çıkarılan faktörlerin açıkladığı varyansı gösterir.

• Rotation Sums of Squared Loadings kısmı, döndürme sonrası daha dengeli açıklanan varyansı gösterir.

Tablodan bakarsak:

• Bileşen 1 = %36.6, Bileşen 2 = %25.0, Bileşen 3 = %23.2

• İlk üç bileşen birlikte toplam %84.8 varyansı açıklıyor.

• Bu da veri setindeki varyansın çok büyük kısmının üç faktörle temsil edilebildiğini gösteriyor.

Sonuç:

• Faktör analizi sonucunda 3 faktörlü bir çözüm uygun görünüyor.

• Döndürme sonrası varyans dağılımı daha dengeli (her faktör daha net ayrılmış).

• faktörden itibaren varyans %13’ün altına düştüğü için dikkate alınmıyor.

SPSS Uygulamalı Faktör Analizi – Bileşen Matrisi (Component Matrix)

Yorum:

• Tablo, her bir değişkenin (X1–X6) üç faktöre (bileşene) göre yük değerlerini (factor loadings) gösteriyor.

• Yük değerleri (factor loadings) ne kadar yüksekse (±0.50 ve üstü), değişkenin o faktörü temsil etme gücü o kadar fazladır.

Tablodan bakarsak:

• Faktör 1: X2 (.906), X3 (.856), X4 (.524) → Birinci faktör bu üç değişkeni güçlü açıklıyor.

• Faktör 2: X6 (.867), X5 (.763) → İkinci faktör bu iki değişkenden etkileniyor.

• Faktör 3: X1 (.793), X5 (.596), X3 (.414) → Üçüncü faktör X1’i güçlü açıklıyor, X5 ve X3 orta düzeyde yüklenmiş.

Sonuç:

• Değişkenler üç ana faktör altında toplanmış durumda.

• Faktör 1 muhtemelen nüfus/ekonomik faaliyet boyutu, Faktör 2 iklim/yağış boyutu, Faktör 3 ise hava kirliliği (SO₂) boyutunu temsil ediyor olabilir.

• X5’in iki faktörde de yük alması çapraz yükleme (cross-loading) anlamına gelir ve dikkatle yorumlanmalıdır.

SPSS Uygulamalı Faktör Analizi – Yeniden Üretilmiş Korelasyonlar (Reproduced Correlations)

Yorum:

• Üst Kısım (Reproduced Correlation): Faktör analizi ile elde edilen modelin tahmin ettiği korelasyon değerlerini gösterir. Örneğin X2 ve X3 arasındaki tahmini korelasyon 0.965’tir. Bu değerler faktör modelinin veriyi ne kadar iyi temsil ettiğini anlamamız için kullanılır.

• Alt Kısım (Residual): Gözlenen korelasyonlarla modelin tahmin ettiği korelasyonlar arasındaki farklardır (artıklar). Fark ne kadar küçükse model veriyi o kadar iyi temsil ediyor demektir.

• Önemli Not: Tablonun altındaki açıklamaya göre 5 (yani %33,0) hücrede artık (residual) değeri 0.05’in üzerinde. Bu, modelin bazı değişken çiftlerinde ilişkileri yeterince iyi açıklamadığını gösterir, ancak genel olarak modelin kabul edilebilir bir uyum sağladığını söyleyebiliriz.

Sonuç: Faktör analizi modeli genel olarak değişkenler arası ilişkileri açıklamada başarılı görünse de bazı değişken çiftlerinde (özellikle X4 ile diğerleri) açıklama gücü düşüktür. Bu, modelin belki de daha fazla faktör veya farklı bir rotasyon yöntemiyle iyileştirilebileceğini gösterir.

SPSS Uygulamalı Faktör Analizi – Döndürülmüş Bileşen Matrisi (Rotated Component Matrix)

Yorum:

• Amaç: Varimax rotasyonu, faktör yüklerini basitleştirerek her değişkenin daha net bir şekilde hangi faktöre ait olduğunu görmemizi sağlar.

• Faktör 1:

  • X3 (.988) ve X2 (.968) bu faktörde çok yüksek yüklenmiş.

  • Bu faktör; üretim, sanayi veya nüfus gibi değişkenlerin temsil ettiği “Sanayi/Nüfus Yoğunluğu” faktörü olabilir.

• Faktör 2:

  • X1 (-.938) ve X4 (.606) bu faktörde yüksek yüklenmiş.

  • Bu faktör; iklim/meteorolojik koşullar (sıcaklık, rüzgâr gibi) etkisini yansıtıyor olabilir.

• Faktör 3:

  • X5 (.923) ve X6 (.788) bu faktörde yüksek yüklenmiş.

  • Bu faktör; yağış ve gün sayısı gibi “Precipitation/İklimsel Etkinlik” faktörü olabilir.

• Genel Değerlendirme:

  • Her değişken daha net bir şekilde bir faktöre ayrıldığı için üç faktörlü çözüm uygun görünüyor.

  • Bu yapı, hava kirliliğini etkileyen faktörleri üç ana boyutta inceleyebileceğimizi gösteriyor: Sanayi/Nüfus Yoğunluğu, İklim ve Yağış.

SPSS Uygulamalı Faktör Analizi – Bileşen Dönüştürme Matrisi (Component Transformation Matrix)

Yorum:

• Bu tablo, Varimax rotasyonunun faktör eksenlerini nasıl dönüştürdüğünü gösterir.

• Satırlar (1, 2, 3) orijinal faktör eksenlerini, sütunlar (1, 2, 3) ise rotasyondan sonraki yeni faktör eksenlerini temsil eder.

• Her hücredeki değer, orijinal faktör ekseni ile yeni faktör ekseni arasındaki korelasyon katsayısıdır.

Ana Noktalar:

• Yüksek değerler (0,8 ve üzeri) her bir bileşenin hangi yeni eksene daha güçlü taşındığını gösterir.

• Örneğin:

  • Orijinal 1. bileşen büyük ölçüde yeni 1. bileşene (.837) taşınmış.

  • Orijinal 2. bileşen büyük ölçüde yeni 3. bileşene (.919) taşınmış.

  • Orijinal 3. bileşen büyük ölçüde yeni 2. bileşene (-.797) taşınmış.

• Bu dönüşüm, faktörlerin birbirinden daha bağımsız ve daha yorumlanabilir hale gelmesini sağlar.

Döndürülmüş Bileşen Uzayında Faktör Dağılımı (Component Plot)

Ne Olduğu:

• Faktör analizi veya temel bileşenler analizinde (PCA), her değişkenin elde edilen faktörlerle (bileşenlerle) ilişkisini görsel olarak gösterir.

• Bu grafik üç boyutlu bir eksende (Component 1, Component 2, Component 3) değişkenlerin konumunu göstererek hangi değişkenin hangi faktöre daha güçlü yüklendiğini anlamamızı sağlar.

Amacı:

• Faktör yapısını görselleştirmek: Hangi değişkenlerin bir arada gruplaştığını gösterir.

• Faktör yorumunu kolaylaştırmak: Benzer faktör yüklerine sahip değişkenlerin birbirine yakın göründüğü için hangi faktörün neyi temsil ettiğini daha kolay kavrayabiliriz.

• Faktör ayrışmasını kontrol etmek: Döndürülmüş grafikte değişkenler daha net gruplara ayrıldığı için faktör çözümünüzün uygunluğunu test edebilirsiniz.

🔹 Genel Bakış

Grafik, X1 – X6 değişkenlerinin üç faktöre (Component 1, Component 2, Component 3) göre konumlarını gösteriyor. SPSS, Varimax rotasyonu sonrası her değişkenin hangi faktörle daha güçlü ilişkili olduğunu bu şekilde görselleştirir.

🔹 Yorum Adımları

1. Gruplaşma Eğilimleri:

   • X2 ve X3 birinci faktöre çok yakın ve aynı bölgede konumlanmış. Bu da bu iki değişkenin aynı yapıyı (faktörü) ölçtüğünü gösterir.

   • X5 ve X6 üçüncü faktöre yakın ve birbirine oldukça yakın konumlanmış. Bu değişkenler de benzer bir yapıyı temsil ediyor.

   • X1 ikinci faktöre daha yakın konumlanmış.

   • X4 ise birinci faktörle orta düzeyde ilişkilidir ancak ikinci faktöre de bir miktar yüklenmiş görünüyor.

2. Faktör Yüklerinin Anlamı:

   • Birinci Faktör: X2 ve X3 üzerinden tanımlanıyor. Bu faktör, bu iki değişkenin temsil ettiği ortak yapıyı açıklıyor.

   • İkinci Faktör: X1 üzerinden tanımlanıyor ve X4’ün de kısmen yüklenmesi var.

   • Üçüncü Faktör: X5 ve X6 üzerinden tanımlanıyor.

3. Faktör Ayrışmasının Kalitesi:

   • Değişkenler birbirinden net ayrıştığı için faktör çözümü yorumlanabilir durumda.

   • Döndürme (Varimax) işlemi bu netliği artırmış; değişkenler birden fazla faktöre dağılmak yerine bir faktörde yoğunlaşmış görünüyor.

🔹 Sonuç

• Bu grafik faktör analizi sonucunda değişkenlerin hangi faktörlerle en güçlü ilişkili olduğunu görselleştiriyor.

• X2 ve X3 birinci faktör; X1 ve kısmen X4 ikinci faktör; X5 ve X6 üçüncü faktör altında toplanarak üç faktörlü bir yapı ortaya koymuş.

• Bu tablo, verinizdeki değişkenlerin nasıl kümelendiğini ve hangi gizli yapılar (latent faktörler) tarafından temsil edildiklerini anlamanıza yardımcı olur.

Gerçekleştirdiğimiz faktör analizi sürecine ait tüm SPSS çıktılarına aşağıdaki bağlantıdan ulaşarak ayrıntılı şekilde inceleyebilirsiniz.

SPSS Uygulamalı Faktör Analizi SPSS Çıktısı.pdf

PDF dosyasını indir • 565KB