Pearson Korelasyon Testi: İki Nicel Değişken Arasındaki Doğrusal İlişkiyi Anlama
- Nominal Analiz
- 29 Tem 2025
- 2 dakikada okunur
1. Testin Amacı
Pearson korelasyon analizi, aynı kaynaktan toplanmış iki nicel değişken arasındaki doğrusal ilişkinin yönünü (+/–) ve gücünü (r) ölçer. Katsayı –1 ≤ r ≤ +1 aralığındadır;
+ işareti: değişkenler birlikte artar / azalır (pozitif ilişki).
– işareti: biri artarken diğeri azalır (negatif ilişki).
|r| ≈ 0: doğrusal ilişki yok; |r| → 1: güçlü doğrusal ilişki vardır.
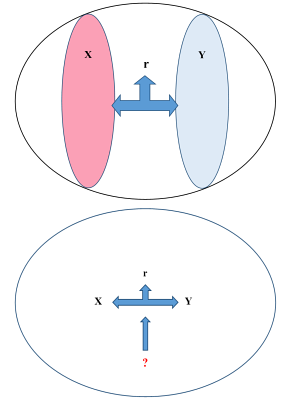
Önemli: Korelasyon nedensellik göstermez; yalnızca birlikte değişimi sayısallaştırır.
2. Ne Zaman Kullanılır?
IQ puanı ↔ sınav başarısı, tansiyon ↔ yaş, gelir ↔ harcama gibi iki sürekli değişkenin ilişkisini incelemek.
Değişkenler aynı birimlerden (birey, kurum, cihaz vb.) eşleştirilmiş olarak ölçülmüş olmalıdır.
3. Varsayımlar
Örneklem rastgele seçilmiştir.
Her iki değişken en az aralık ölçeğindedir.
Değişkenler yaklaşık normal dağılır.
Ölçümler bağımlıdır (aynı gruba ait) ancak değişkenler birbirinden bağımsızdır (biri diğerini doğrudan etkilemez).
Varsayımlar sağlanmıyorsa Spearman sıralı korelasyon testi tercih edilir.
4. Katsayının Hesaplanması
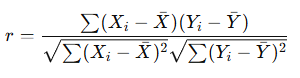
r = 0 → doğrusal ilişki yok
r = ±1 → mükemmel doğrusal ilişki
5. Sonuçların Yorumlanması
| |r| Aralığı | Etki Büyüklüğü*
||---|-----------|----------------|
| 0,10 – 0,29 | Küçük |
| 0,30 – 0,49 | Orta |
| 0,50 – 1,00 | Büyük |
*Cohen (1988) önerisine dayalı genel kılavuz; alana göre esneklik gerekir.
p < 0,05 → İlişki istatistiksel olarak anlamlıdır.
p > 0,05 → Anlamlı ilişki yoktur.
6. Determinasyon Katsayısı (r²)
r², değişkenlerden birindeki varyansın yüzde kaçının diğer değişkenle paylaşıldığını gösterir. Örneğin r = 0,60 ise r² = 0,36 → değişimin %36’sı ortak açıklanır.
7. Korelasyon ≠ Nedensellik
Korelasyon yön vermez; X → Y mi, Y → X mi bilinmez.
Üçüncü değişken sorunu: Başka faktörler hem X’i hem Y’yi etkileyebilir (ör. çalışma süresi, motivasyon).
Nedensel yorum için deneysel tasarım, regresyon modelleri veya kontrol değişkenli kısmi korelasyon gerekir.
8. Parametrik Olmayan Alternatif
Spearman rho: Veriler sıralı ölçekliyse veya normal dağılım varsayımı bozulmuşsa kullanılır.
Yorumu r ile aynıdır; katsayı –1 ≤ ρ ≤ +1 aralığındadır.
9. Yaygın Hatalar & İpuçları
Nedensellik iddiası: Yalnızca korelasyonla “X, Y’ye sebep olur” denemez.
Outlier etkisi: Aykırı değerler r’yi abartabilir veya maskeler. Kutu grafiğiyle kontrol edin.
Nonlineer ilişki gözden kaçabilir: r yalnızca doğrusal bağıntıyı yakalar. Saçılım diyagramı inceleyin.
Çoklu karşılaştırma: Birden çok korelasyon test ediliyorsa Bonferroni veya FDR düzeltmesi uygulayın.
10. Dikkat Edilmesi Gerekenler
Değişkenler sürekli mi?
Aynı örneklemden mi?
Normal dağılım kabaca sağlanıyor mu?
Aykırı değer var mı?
Saçılım grafiği doğrusal mı?
p değeri ve r büyüklüğü raporlandı mı?
r² ile açıklanan varyans sunuldu mu?








Yorumlar