Normal Dağılım: Tanımı, Özellikleri, Değerlendirme Kriterleri ve SPSS Uygulama Kılavuzu

1. Normal Dağılım Nedir?

Normal dağılım, doğadaki pek çok nicel değişkenin dağılımını temsil eden ve istatistikte en sık karşılaşılan dağılım türüdür. Matematiksel olarak ilk kez Gauss tarafından tanımlanan bu dağılım, toplum veya doğadan rastgele seçilmiş bir nicel değişkenin değerlerinin simetrik bir “çan eğrisi” şeklinde dağıldığını kabul eder. Normal dağılım, istatistik teorisinin temelini oluşturur ve özellikle Merkezi Limit Teoremi ile desteklenmektedir.

2. Normal Dağılımın Temel Özellikleri

• Ortalama = Ortanca = Mod: Teorik olarak normal dağılımda bu üç ölçü aynıdır.

• Simetrik Dağılım: Çan eğrisi ortalama etrafında simetrik yayılır.

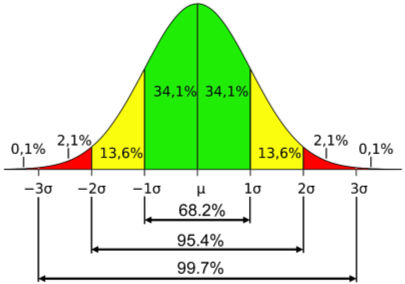
• Standart Sapma ve Dağılım Aralıkları:

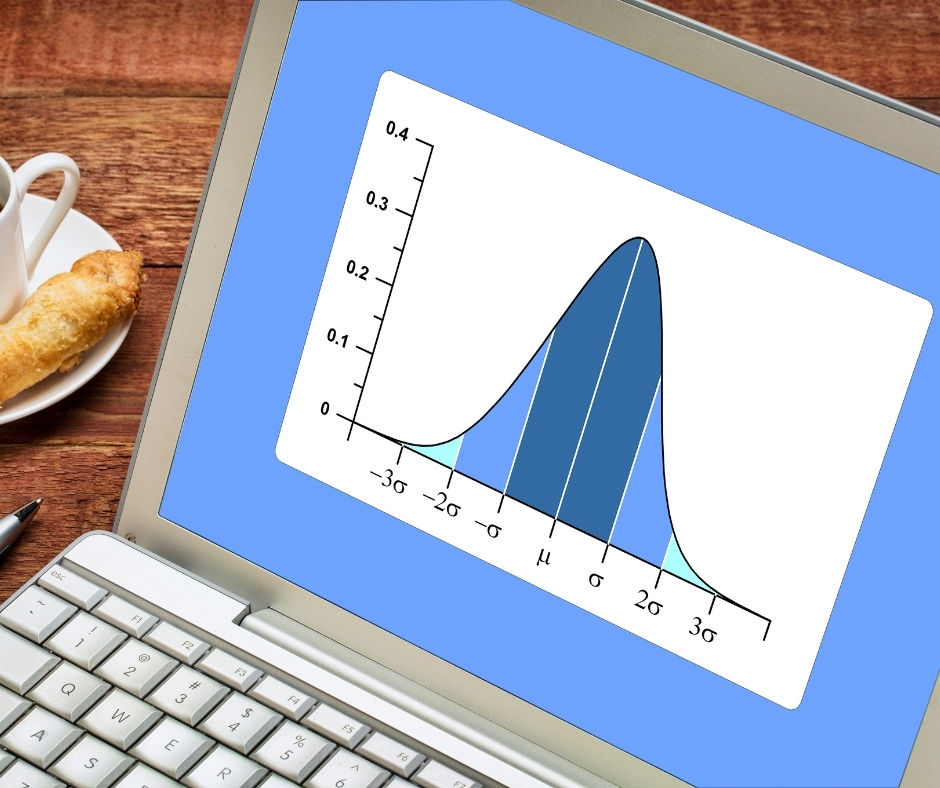
  • Tüm değerlerin yaklaşık %68,26’sı ortalama ±1 standart sapma aralığındadır.

  • %95,44’ü ortalama ±2 standart sapma,

  • %99,74’ü ise ortalama ±3 standart sapma içerisindedir.

• Çan Eğrisi: Değerlerin büyük bölümü ortalama civarında yoğunlaşır; uçlarda ise azalma görülür.

3. Normal Dağılımı Etkileyen Faktörler ve Merkezi Limit Teoremi

Normal dağılım, rastgele seçilen bir örneklemin ölçümlerinin, örneklem büyüklüğü yeterince büyük olduğunda (genellikle n≥30), normal dağılıma yaklaşacağını öngören Merkezi Limit Teoremi ile açıklanır.

Bu nedenle, örneklem büyüklüğünün 30 ve üzerinde olması genellikle normal dağılımın sağlanması için yeterli kabul edilir. Ancak güncel araştırmalar, daha küçük örneklemlerde de normal dağılıma yaklaşılabileceğini, büyük örneklemlerde ise bazen sağlanamayabileceğini göstermiştir.

4. Normal Dağılımın Değerlendirilmesi: Kriterler

Bir nicel değişkenin normal dağılım sergileyip sergilemediğini değerlendirmek için aşağıdaki kriterler dikkate alınmalıdır:

4.1. Görsel ve Tanımlayıcı Kriterler

• Ortalama, ortanca ve mod değerlerinin birbirine yakın olması.

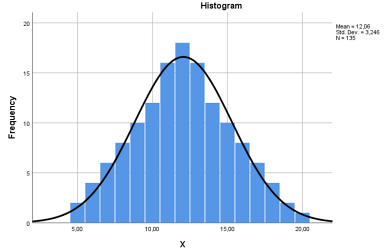
• Histogram dağılımının çan eğrisi şeklinde ve simetrik olması.

• Çarpıklık (Skewness) ve Basıklık (Kurtosis) katsayılarının -1 ile +1 arasında olması (literatürde yaygın kullanılan referans aralık).

  • Skewness negatifse dağılım sağa çarpıktır, pozitifse sola çarpıktır.

  • Kurtosis negatifse dağılım basık, pozitifse sivridir.

  • Her iki katsayının sıfıra yakın olması ideal normal dağılıma işaret eder.

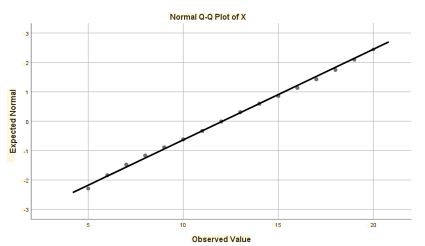
• Normal Q-Q Plot: Gözlenen değerlerin, teorik normal değerlerle örtüşerek yaklaşık 45 derecelik bir doğru üzerinde sıralanması beklenir.

4.2. İstatistiksel Testler

Normal dağılımı test etmek için iki temel yöntem kullanılır:

• Shapiro-Wilk Testi: Örneklem büyüklüğü n<30 ise tercih edilir; küçük örneklemlerde duyarlıdır.

• Kolmogorov-Smirnov Testi: n≥30 durumunda uygulanır; büyük örneklemler için standarttır.

Testlerin sonuçlarına göre:

• p > 0,05: Normal dağılım varsayımı sağlanır.

• p < 0,05: Normal dağılım varsayımı sağlanmaz.

Not: Testlerin p-değeri kesin karar için yeterli değildir. Daima histogram, Q-Q Plot ve tanımlayıcı istatistikler gibi ek kriterlerle değerlendirilmelidir.

5. Normal Dağılımın Analizlerdeki Önemi

Normal dağılımın sağlanıp sağlanmaması, kullanılacak istatistiksel analiz yöntemlerinin seçilmesinde belirleyicidir:

• Normal dağılım varsa: Parametrik testler (t-testi, ANOVA vb.) kullanılabilir. Merkezi eğilim ve yayılım ölçüleri olarak ortalama, standart sapma, minimum ve maksimum raporlanır.

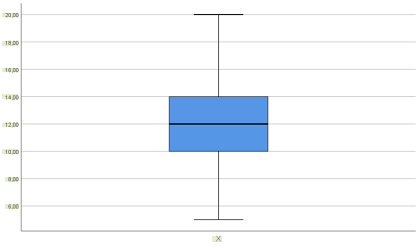
• Normal dağılım yoksa: Non-parametrik testler (Mann-Whitney U, Kruskal-Wallis vb.) tercih edilir. Merkezi eğilim ve yayılım ölçüleri olarak ortanca, çeyrekler (Q1, Q3), minimum ve maksimum raporlanır.

6. SPSS’te Normal Dağılım Analizi: Uygulama Kılavuzu

6.1. Explore Menüsüyle Normal Dağılım Testi

1. Analyze menüsünden Descriptive Statistics > Explore seçeneğine girin.

2. Analiz etmek istediğiniz nicel değişkenleri “Dependent List” bölümüne aktarın.

3. (Varsa) Kategorik gruplar için “Factor List” bölümünü kullanın.

4. Plots bölümüne tıklayarak “Histogram” ve “Normality plots with tests” seçeneklerini işaretleyin.

5. “Continue” ve ardından “OK” tuşuna basın.

6. Sonuç ekranında;

   • Descriptive Statistics tablosunda ortalama, ortanca, mod, standart sapma, çarpıklık, basıklık gibi özet istatistikler,

   • Tests of Normality tablosunda Shapiro-Wilk ve Kolmogorov-Smirnov sonuçları,

   • Histogram ve Q-Q Plot grafiklerinde dağılım yapısı görüntülenir.

6.2. Histogram ve Mod Görüntüleme (Frequencies)

1. Analyze > Descriptive Statistics > Frequencies menüsüne girin.

2. Nicel değişkenleri “Variables” bölümüne aktarın.

3. Statistics butonundan “Mod” seçeneğini işaretleyin.

4. Charts butonundan “Histogram” ve “Show normal curve on histogram” seçeneklerini işaretleyin.

5. “OK” tuşuna basarak işlemi tamamlayın.

7. Sonuçların Yorumlanması

• Eğer p>0,05 ve çarpıklık/basıklık -1 ile +1 arasındaysa, Q-Q Plot’ta noktalar doğruya yakınsa ve histogram çan eğrisine benziyorsa; değişkeniniz normal dağılım göstermektedir.

• Eğer bu kriterlerden biri veya birkaçı sağlanmıyorsa, değişken normal dağılım göstermiyor kabul edilir.

8. Özet ve Sonuç

Normal dağılım, bilimsel araştırmalarda istatistiksel analizlerin temel varsayımlarından biridir. Bu nedenle, nicel veriler üzerinde analiz öncesi mutlaka normal dağılıma uygunluk kontrol edilmeli, sonuçlara göre doğru analiz yöntemleri seçilmelidir. SPSS programı ile görsel ve istatistiksel yöntemlerle kolayca normal dağılım analizi yapılabilir.