Bağımsız Gruplarda t Testi ve Mann-Whitney U Testi: Temel Kavramlar, Hipotezler ve Etki Büyüklüğü

1. Bağımsız Gruplarda t Testi Nedir?

Bağımsız Gruplarda t Testi (Independent Samples T-Test), iki bağımsız grubun bir nicel (sayısal) değişken üzerindeki ortalamalarının istatistiksel olarak anlamlı bir şekilde farklı olup olmadığını sınamak için kullanılan bir parametrik testtir.

• Örnek: Kadın ve erkek öğrencilerin sınav puanlarının karşılaştırılması.

Bu testte temel olarak, iki farklı grubun ölçülen bir değişken bakımından birbirinden anlamlı bir biçimde farklı olup olmadığı araştırılır.

Varsayımlar (Koşullar):

• Gruplar birbirinden bağımsız olmalı (bir birey birden fazla grupta yer almamalı).

• Her iki gruptaki örneklem, evrenden tesadüfi (random) seçilmiş olmalı.

• Bağımlı değişken en az aralık ölçeğinde ölçülmeli (örn. puan, kilo, süre).

• Her iki gruptaki veriler normal dağılım göstermeli.

• Grupların varyansları eşit olmalı (bu, Levene’s Test ile sınanır).

Esnek Varsayım:

• Eğer her grupta en az 10 kişi varsa ve örneklem tesadüfi seçildiyse, değişkenin tüm örneklemde normal dağılması çoğu durumda yeterli görülür.

• Varyansların eşitliği zorunlu değildir, test iki durumda da sonuç verir.

2. Non-Parametrik Alternatif: Mann-Whitney U Testi

Eğer gruplar arası bağımlı değişkenin dağılımı normal değilse veya ölçek düzeyi en az aralık değilse, parametrik testler yerine non-parametrik bir yöntem olan Mann-Whitney U Testi uygulanır.

• Mann-Whitney U Testi, iki bağımsız grubun ortalamalarını değil, sıralarını karşılaştırır.

• Yani, gruplar arasındaki “ortalama” fark yerine, “sıralama” farkı araştırılır.

• Verilerde uç değer (aykırı değer) olduğunda veya dağılım normal değilse daha güvenilirdir.

3. Hipotezler

Her iki testte de benzer şekilde hipotezler kurulur:

H0 (Null Hipotez): İki grubun ortalaması (ya da sıralaması) arasında anlamlı bir fark yoktur.

H1 (Alternatif Hipotez): İki grubun ortalaması (ya da sıralaması) arasında anlamlı bir fark vardır.

Karar Kuralları:

• p > 0,05 ise: H0 kabul edilir → Anlamlı fark yoktur.

• p < 0,05 ise: H0 reddedilir → Anlamlı fark vardır.

4. Etki Büyüklüğü (Effect Size)

Bir hipotez testinde sadece farkın olup olmadığını bilmek yeterli değildir; farkın ne kadar büyük/önemli olduğu da bilinmelidir. İşte burada etki büyüklüğü devreye girer.

Neden Etki Büyüklüğü?

• Sadece p-değeri ile sonuca varmak yanıltıcı olabilir. Çünkü çok büyük örneklemlerde küçük farklar da anlamlı çıkabilir.

• Etki büyüklüğü, bulduğun farkın istatistiksel olarak değil, pratikte ne kadar önemli olduğunu gösterir.

Sık Kullanılan Etki Büyüklüğü Ölçütleri

A-) Eta Kare (η²): Bağımsız değişkenin bağımlı değişken üzerindeki toplam varyansın ne kadarını açıkladığını gösterir.

1. 0 ile 1 arasında değer alır.

2. 0,01 küçük, 0,06 orta, 0,14 büyük etki olarak değerlendirilir.

Örneğin, η² = 0,14 ise, bağımsız değişken bağımlı değişkendeki varyansın %14’ünü açıklıyor demektir.

Formül:

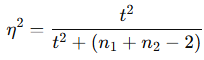
B-) r Etki Büyüklüğü (Korelasyon Katsayısı): Doğrusal ilişkinin gücünü gösterir. r değeri 0 (etki yok) ile 1 (mükemmel etki) arasındadır.

• 0,10 küçük, 0,30 orta, 0,50 büyük etki olarak değerlendirilir.

Formül:

C-) Cohen’s d: Gruplar arasındaki ortalama farkın, standart sapmaya oranını verir.

• 0,2 küçük, 0,5 orta, 0,8 büyük etki olarak değerlendirilir.

• Yani, ortalamalar arasında 0,8 standart sapmalık fark varsa bu büyük bir etkidir.

Formül:

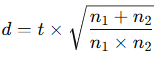
5. Yorumlama ve Uygulama Örnekleri

• Örnek 1: Kadın ve erkeklerin depresyon puanlarının karşılaştırılması.Eğer veriler normal dağılıma uygunsa bağımsız gruplarda t testi, normal değilse Mann-Whitney U testi uygulanır.

• Örnek 2: Kadın ve erkeklerin aylık gelir ortalamaları.Verilerin dağılımına ve ölçek tipine göre uygun test seçilerek anlamlılık ve etki büyüklüğü birlikte değerlendirilir.

6. Önemli Notlar

• Karşılaştırılan gruplarda öncelikle normal dağılım varsayımı kontrol edilmelidir.

• Hipotez testi ile fark bulunursa, etki büyüklüğü hesaplanıp mutlaka rapor edilmelidir.

• Etki büyüklüğü (η², r, d), sonucun uygulamadaki önemini gösterir.

• Yorumda sadece p değeri değil, etki büyüklüğü de dikkate alınmalıdır.

Bağımsız Gruplarda t Testi ve Mann-Whitney U Testi, iki grup arasındaki farkın anlamlı olup olmadığını test etmek için kullanılan temel yöntemlerdir. Anlamlı fark bulunsa dahi, bu farkın büyüklüğünü ve pratikteki önemini anlamak için mutlaka etki büyüklüğü de hesaplanmalı ve yorumlanmalıdır. Araştırmalarda yalnızca istatistiksel anlamlılık değil, bulguların gerçek hayattaki anlamı da göz önünde bulundurulmalıdır.